
© Ivana Martic, MATH+
Autor*innen: Moritz Grillo, Martin Skutella
Projekt: AA3-12: On the Expressivity of Neural Networks
Aufgabe
Vor langer Zeit gab es eine Geschichte von drei Weisen, die von einem Stern zu einem bestimmten Ort geführt wurden – eine Erzählung, die über Generationen weitergegeben wurde.
Diese Idee mit dem Stern und den drei Weisen aus dem Morgenland hatte dem Abiturienten Geoffrey noch nie eingeleuchtet. Nicht, dass er den teils hanebüchenen Rest der Geschichte geglaubt hätte — in seinen Augen eine 2000 Jahre alte ‘Urban Legend’. Aber die Sache mit dem Stern ließ ihm keine Ruhe. Zwar war Lichtverschmutzung vor 2000 Jahren wohl noch kein Thema, aber selbst bei klarem Sternenhimmel: Wie soll bitte ein weit entfernter Stern oder Komet den Weisen den genauen Weg gewiesen haben?
Daher beschloss Geoffrey gemeinsam mit seinem Freund John, das diesjährige Krippenspiel aufzupeppen und den heiligen drei Königen mit künstlicher Intelligenz den Weg zur Krippe zu weisen. Dazu hatten die beiden ein kleines neuronales Netz entwickelt, das sie in Form einer Handy-App an die vom Dorfpfarrer handverlesenen Darsteller der drei Könige verteilen wollten. Allerdings machten die drei weder einen weisen, geschweige denn einen heiligen Eindruck.
Umso interessierter zeigte sich Chantalle, die Darstellerin der heiligen Jungfrau Maria. Sie hatte laut Regie-Anweisung des Dorfpfarrers nur fromm zu schauen und das Reden ihrem Gatten Josef zu überlassen. Frustriert von dieser veralteten Rollenverteilung beschloss Chantalle, ihre Energie anderweitig einzusetzen: Sie half dabei, sicherzustellen, dass die sogenannten ‘Weisen’ tatsächlich ihren Weg zum Zielort fanden – ein nicht ganz uneigennütziger Gedanke, da sie selbst schnellstmöglich aus dem ihr auferlegten frommen Dasein erlöst werden wollte.
“Die Sache ist eigentlich ganz einfach”, erklärte ihr John. “Man gibt die x– und y-Koordinate des eigenen Standorts in das neuronale Netz ein, das dann einen nicht-negativen Wert z ausgibt. Je größer z ist, desto näher ist man an der Krippe”.
“Und wie berechnet das neuronale Netz dieses z?”, fragte Chantalle neugierig, “und bei welchem Wert z hat man die Krippe erreicht?”
Bereitwillig zeigte Geoffrey ihr eine detaillierte Skizze vom Innenleben des neuronalen Netzes:
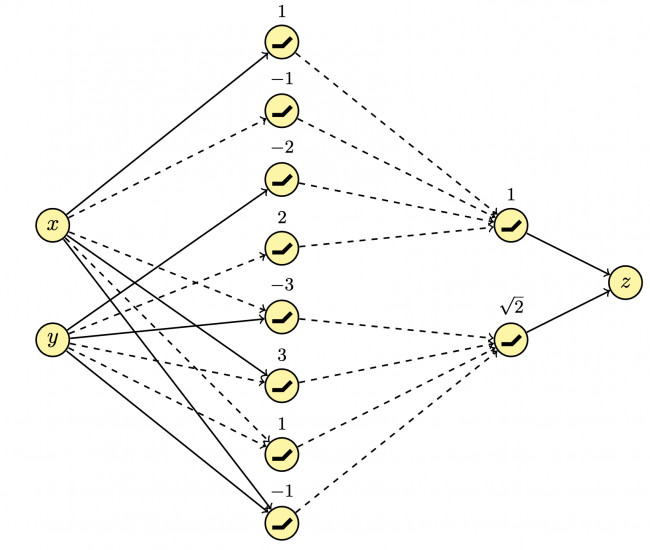
“Das Netz besteht aus untereinander verbundenen Neuronen”, erläuterte Geoffrey, “die hier durch gelbe Kreise und die Verbindungen durch Pfeile dargestellt sind. Die mit x und y beschrifteten Neuronen auf der linken Seite sind Input-Neuronen, deren Werte auf die x– und y-Koordinate gesetzt werden. Das mit z beschriftete Output-Neuron auf der rechten Seite gibt den Wert z aus. Dazwischen gibt es zwei Schichten mit versteckten Neuronen, in denen die eigentliche Berechnung stattfindet. Die erste Schicht besteht hier aus acht und die zweite aus zwei versteckten Neuronen.”
John fuhr fort: “Um die Werte der Neuronen einer Schicht zu berechnen, muss man zunächst die Werte der Neuronen der vorherigen Schicht kennen, die dann über die Pfeile an die nächste Schicht übertragen werden. Ein durchgezogener Pfeil sendet den Wert eines Neurons an das Neuron in der nächsten Schicht. Auch ein gestrichelter Pfeil überträgt diesen Wert, dreht dabei allerdings das Vorzeichen um, d.h. multipliziert ihn mit -1. Das empfangende Neuron addiert alle auf eingehenden Pfeilen übertragenen Werte zu der über dem Neuron angegebenen Zahl. Der Wert des empfangenden Neurons ist dann das Maximum von 0 und dieser Summe. Sind x und y die Werte der beiden Input-Neuronen, so ergeben sich beispielsweise die Werte der acht versteckten Neuronen in der ersten Schicht zu (von oben nach unten)
\max\{0,x+1\}
\max\{0,-x-1\}
\max\{0,y-2\}
\max\{0,-y+2\}
\max\{0,-x+y-3\}
\max\{0,x-y+3\}
\max\{0,-x-y+1\}
\max\{0,x+y-1\}
Die Werte der beiden versteckten Neuronen der zweiten Schicht ergeben sich nach derselben Regel aus den Werten der versteckten Neuronen der ersten Schicht. Der am Ende ausgegebene Wert z des Output-Neurons ist die Summe der Werte der beiden versteckten Neuronen aus der zweiten Schicht.”
Fasziniert studierte Chantalle die Skizze und versuchte zu verstehen, was die intuitive Bedeutung der einzelnen Neuronen des Netzes ist. Geoffrey gab ihr den Tipp herauszufinden, für welche Koordinatenpaare x,~y die beiden versteckten Neuronen der zweiten Schicht einen echt positiven Wert annehmen. “Daraus ergibt sich dann unmittelbar, für welche Paare x,~y der resultierende Output z echt positiv ist”, sagte er. Als Chantalle schließlich ein sternförmiges Gebilde auf ihren Zettel zeichnete, wusste Geoffrey, dass sie es verstanden hatte.
“Und jetzt weiß ich auch, bei welchem Koordinatenpaar (x,y) die drei Könige die Krippe finden, und wie groß der dort erreichte maximale Wert für z ist”, sagte Chantalle, und ihr frommer Blick wich einem zufriedenen Grinsen.
Aufgabenstellung
Finde heraus
i) welche der Skizzen S1 bis S9 in Abbildung 1a) korrekt ist,
ii) welcher der Werte W1 bis W9 in Abbildung 1b) der korrekte Maximalwert für z ist, und
iii) für welches Koordinatenpaar P1 bis P9 in Abbildung 1c) der Maximalwert für z angenommen wird.
a) Mögliche Skizzen des Bereichs in der x–y-Ebene, wo z > 0 (Beachte, dass die Skizzen maßstabsgetreu sind):

b) Mögliche Maximalwerte für z:
W1: 0
W4: 3
W7: \sqrt{2} + 1
W2: 1
W5: 4
W8: \sqrt{2} + 2
W3: 2
W6: \sqrt{2}
W9: 2\sqrt{2}
c) Mögliche Koordinatenpaare (x, y), bei denen z maximal ist:
P1: (0,0)
P4: (2,1)
P7: (1,-2)
P2: (0,1)
P5: (-1,2)
P8: (2,-1)
P3: (1,2)
P6: (-2,1)
P9: (-1,-2)
Abbildung 1: Mögliche Skizzen, Werte und Koordinatenpaare
Bei welcher der Antwortmöglichkeiten 1 bis 10 taucht das korrekte Tripel bestehend aus Skizze, Wert und Koordinatenpaar auf?
Antwortmöglichkeiten:
- (S1,W1,P1) oder (S2,W2,P2) oder (S3,W3,P3) oder (S4,W4,P4)
- (S5,W5,P5) oder (S6,W6,P6) oder (S7,W7,P7) oder (S8,W8,P8)
- (S9,W9,P9) oder (S1,W3,P1) oder (S2,W4,P2) oder (S3,W5,P3)
- (S4,W6,P4) oder (S5,W7,P5) oder (S6,W8,P6) oder (S7,W9,P7)
- (S8,W1,P8) oder (S9,W2,P9) oder (S1,W2,P3) oder (S2,W3,P3)
- (S3,W4,P5) oder (S4,W5,P6) oder (S5,W6,P7) oder (S6,W7,P8)
- (S7,W8,P9) oder (S8,W9,P1) oder (S9,W1,P2) oder (S1,W5,P4)
- (S2,W7,P5) oder (S3,W6,P6) oder (S4,W8,P7) oder (S5,W9,P8)
- (S6,W1,P9) oder (S7,W2,P1) oder (S8,W3,P2) oder (S9,W4,P3)
- (S1,W9,P5) oder (S2,W8,P6) oder (S3,W7,P5) oder (S4,W6,P8)
Projektbezug:
In unserem MATH^+ Forschungsprojekt mit dem Titel On the Expressivity of Neural Networks arbeiten wir an einem besseren strukturellen Verständnis neuronaler Netze. Ähnlich wie Chantalle in unserer Geschichte bemühen wir uns, die Eigenschaften eines gegebenen neuronalen Netzes zu verstehen. Und wir erforschen außerdem, welche Strukturen ein neuronales Netz haben sollte, um bestimmte Funktionen exakt berechnen zu können. Eines unserer Ergebnisse besagt zum Beispiel, dass neuronale Netze mit vielen versteckten Schichten deutlich komplexere Entscheidungsmuster (die Regionen, in denen das neuronale Netz einen positiven Wert annimmt) haben können als neuronale Netze mit wenigen versteckten Schichten.
Vor wenigen Wochen wurden Geoffrey Hinton von der University of Toronto (Kanada) und John Hopfield von der Princeton University (USA) mit dem Nobelpreis ausgezeichnet “für grundlegende Entdeckungen und Erfindungen, die maschinelles Lernen mit künstlichen neuronalen Netzwerken ermöglichen“.