16 Die Zahlen von Nazareth

Autor: Matthew Maat (Universität Twente)

Projekt: Combining algorithms for parity games and linear programming

Aufgabe

Im kleinen Dorf Nazareth, siehe Abbildung 1(i), gibt es nur sechs Straßen. Es ist möglich, einen Kreis zu gehen, das heißt, man läuft über eine Reihe von Straßen und kehrt zum Ausgangspunkt zurück (ohne eine Kreuzung zweimal zu überqueren). Zum Beispiel bilden die Straßen $a$ , $d$ und $f$ einen Kreis. Wir bezeichnen diesen Kreis als $(adf)$ . Insgesamt gibt es sieben Kreise, die anderen sind $(bde), (cef), (abc), (adec), (abef)$ und $(bcfd)$ . Beachte, dass die Startposition eines Kreises keine Rolle spielt, z. B. werden die Kreise $(adf)$ und $(dfa)$ als derselbe Kreis betrachtet.

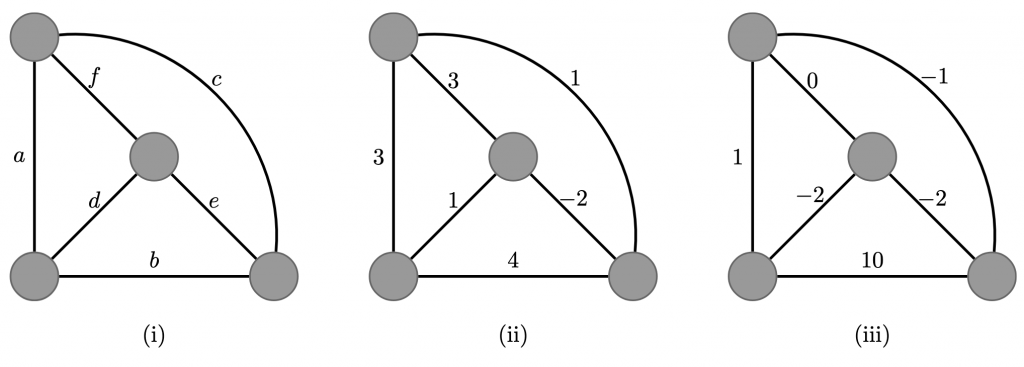
Abbildung 1: Die Straßen von Nazareth

Nun spielen Joseph und Maria ein Spiel namens “Nummeriere die Straßen”. Jede Runde beginnt damit, dass der Dorfälteste eine Menge von Kreisen bekannt gibt.
Maria und Josef haben eine Karte des Dorfs. Sie schreiben jeweils sechs ganze Zahlen auf die eingezeichneten Straßen in der Karte.

Joseph erhält einen Punkt, wenn folgenden Bedingungen erfüllt sind:

Für jeden Kreis, den der Älteste vorgab, ist die größte Zahl, die Joseph schrieb, gerade.
Für jeden Kreis, den der Älteste nicht vorgab ist die größte Zahl, die Joseph schrieb, ungerade.

Maria erhält einen Punkt, wenn folgenden Bedingungen erfüllt sind:

In jedem Kreis, den der Älteste ausrief, ist die Summe der Zahlen, die Maria schrieb, mindestens 0.
In allen anderen Kreisen ist die Summe der Zahlen, die Maria schrieb, kleiner als 0.

Joseph und Maria spielen eine Proberunde:
Die Abbildung 1 zeigt Zahlen, welche Joseph (ii) und Maria (iii) geschrieben haben, um einen Punkt in der Runde zu erzielen, in der der Älteste die Straßen $(bde), (abc), (bcfd)$ und $(abef)$ ausgerufen hätte.
Im Kreis $(bde)$ , den der Älteste ausgerufen hat, ist die größte Zahl 4, die tatsächlich gerade ist. Es lässt sich überprüfen, dass die beiden Eigenschaften auch für die anderen sechs Kreise zutreffen.
Bei Maria ist die Summe der Zahlen im Kreis $(bde)$ $10-2-2=6$ , was sogar größer als 0 ist. Es lässt sich ebenfalls überprüfen, dass die anderen sechs Kreise ebenfalls korrekt sind.

Im eigentlichen Spiel werden drei Runden gespielt. Nach jeder Runde streichen Joseph und Maria ihre alten Zahlen durch und überlegen sich neue Zahlen für die nächste Runde. Die erzielten Punkte werden addiert. Der Älteste gibt die folgenden Mengen von Kreisen vor:

Runde 1: $(adf)$ und $(cef)$
Runde 2: $(abc), (bde), (cef)$ und $(adf)$
Runde 3: $(abef)$ und $(bcfd)$

Angenommen, Joseph und Maria spielen bestmöglich. Sei $J$ die Gesamtsumme der Punkte von Joseph und $M$ die von Maria. Was ist das Endergebnis, geschrieben als $J-M$ ?

Antwortmöglichkeiten

$0-3$
$1-3$
$1-1$
$1-2$
$3-3$
$2-1$
$2-2$
$2-3$
$3-0$
$3-1$

Du musst eingeloggt sein, um deine Lösung abzugeben.

Letzte PDF-Aktualisierung: 16.12. 16:45 Uhr, Fehler bei Antwortöglichkeit 5 berichtigt.

Aufgabe als PDF