13 Umgeben von Rubinen

© Julia Nurit Schönnagel, MATH+

Autor: Matthew Maat (Universität Twente)

Project: Combining algorithms for parity games and linear programming

Aufgabe

Irgendwo im Fernen Osten packen die Weisen ihre Geschenke, um sie dem neugeborenen König zu überreichen. Beim Beladen ihrer Kamelbeutel merken sie, dass eine der würfelförmigen Schachteln, die an einigen Ecken mit Rubinen verziert ist, kaputt ist (Abbildung 1, links).

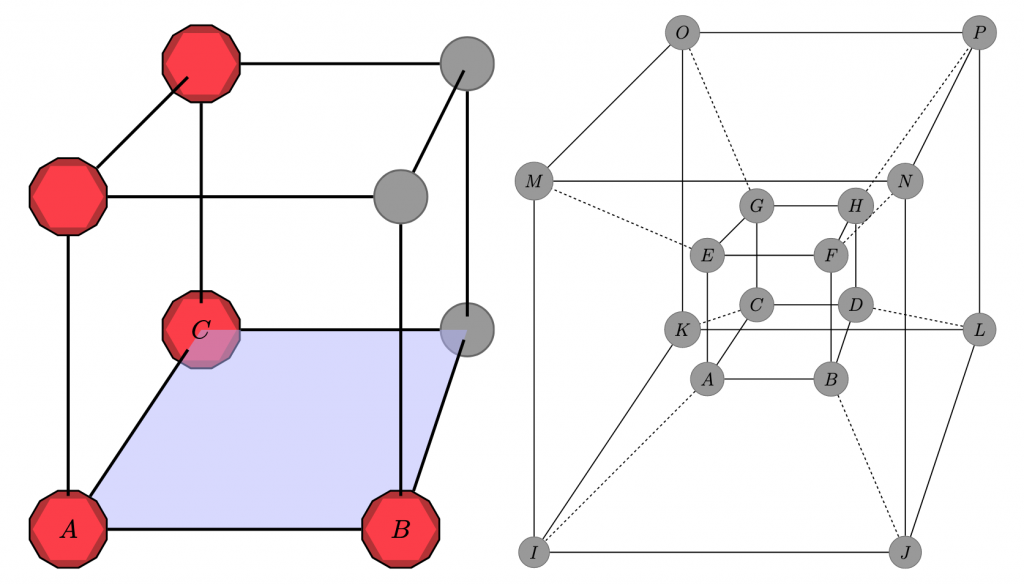
Abbildung 1: Links: Ursprüngliches Design der (jetzt kaputten) Schachtel. Die Rubine sind rot markiert. Rechts: Die Struktur eines Tesserakts.

Der Rubin mit der Markierung A ist abgefallen. Sie finden das Loch im Muster schnell, da sie ein altes östliches Dekorationsmuster verwenden, bei dem die Rubine auf der würfelförmigen Schachtel immer so platziert sind, dass

• alle Rubine durch Kanten verbunden sind,
• die Ecken ohne Rubine, sogenannte Nicht-Rubine, ebenfalls alle durch Kanten verbunden sind,
• und dies für jedes Quadrat (jede Fläche der Schachtel) gilt, d. h. alle Rubine in einem Quadrat und alle Nicht-Rubine sind über Kanten verbunden.

Im blauen Quadrat der kaputten Schachtel ist Rubin B jetzt nicht mehr mit Rubin C verbunden, was zeigt, dass die Schachtel kaputt ist.

Die Weisen stimmen darin überein, dass die alte Schachtel eine gute Möglichkeit hatte, zu erkennen, ob sie kaputt ist, aber sie war nicht perfekt: Zum Beispiel könnte man nicht erkennen, dass die Schachtel kaputt ist, wenn Rubin B statt Rubin A abgefallen wäre. Daher wollen sie die alte Schachtel nicht reparieren, sondern eine neue bauen. Dieses Mal wollen sie einen sogenannten Tesserakt verwenden (einen vierdimensionalen Hyperwürfel, siehe Beschreibung am Ende der Aufgabe).
Sie möchten, dass einige Ecken des Tesserakts Rubine tragen und haben folgende Anforderungen an das Design:

1. Es gibt mindestens einen Rubin im Design.
2. Alle Rubine sind miteinander verbunden (über Folgen von Kanten), und alle Nicht-Rubine sind ebenfalls miteinander verbunden.
3. In jedem Würfel des Tesserakts gilt dasselbe: Alle Rubine sind verbunden, und alle Nicht-Rubine sind verbunden.
4. In jedem Quadrat sind ebenfalls alle Rubine verbunden und die Nicht-Rubine verbunden.
5. Es soll leicht erkennbar sein, ob ein Rubin fehlt: Wenn ein Rubin verschwindet, gibt es ein Quadrat, in dem die Rubine nicht verbunden sind (wie das blaue Quadrat in Abbildung 1, links, wenn Rubin A fehlt). Beachten Sie, dass wir die Rubine auch dann als verbunden ansehen, wenn sich auf einem Quadrat kein Rubin befindet.

Die Weisen denken lange nach und finden ein Design, das nicht nur die Anforderungen erfüllt, sondern auch die meisten Rubine aller Designs hat, die die Anforderungen erfüllen.

Frage: Wie viele Rubine befinden sich auf dem Tesserakt in ihrem Design?

Über den Tesserakt: Genauso wie man einen Würfel erstellen kann, indem man zwei Quadrate nimmt und ihre vier Ecken mit Kanten verbindet, kann man einen Tesserakt (in vier Dimensionen) erstellen, indem man zwei Würfel nimmt und die acht Eckpaare der Würfel verbindet (siehe Abbildung 1, rechts). Ein Tesserakt hat 16 Ecken (A,B,C,\ldots,P), 32 Kanten (zum Beispiel die Kanten AB,~JN und CK), 24 Quadrate (wie ABDC,~IKOM oder JBFN) und 8 Würfel (zum Beispiel bilden A,B,C,D,E,F,G,H einen Würfel und A,B,E,F,I,J,M,N bilden einen Würfel). Da der Tesserakt 4-dimensional ist, handelt es sich bei der Abbildung 1 rechts nur um eine Projektion. Dementsprechend können Quadrate oder auch Würfel verzerrt in der Abbildung erscheinen.

Antwortmöglichkeiten

1. 4 oder weniger Rubine
2. 5 Rubine
3. 6 Rubine
4. 7 Rubine
5. 8 Rubine
6. 9 Rubine
7. 10 Rubine
8. 11 Rubine
9. 12 Rubine
10. 13 oder mehr Rubine