10 Weihnachtsplätzchen ausstechen

© Ivana Martic, MATH+

Autoren: Pim van ‘t Hof, Stefano Piceghello (Universität von Twente)

Projekt: 4TU.AMI

Aufgabe

Die Elfen Pi und Pie backen perfekt runde Weihnachtsplätzchen. Mit einem kreisrunden Plätzchenausstecher schneiden sie vier identische Plätzchen aus einem großen kreisrunden Teig aus. Abbildung 1 zeigt den verbleibenden Teig, nachdem die Plätzchen in den Ofen gelegt wurden. Die Abbildung zeigt außerdem zwei senkrecht zueinander stehende Durchmesser AB und CD des großen Teigkreises. Der Durchmesser AB ist tangential zur Begrenzung eines der kreisförmigen Löcher. Die Strecke EF ist eine Sehne des großen Teigkreises, die ebenfalls tangential zur Begrenzung desselben Loches verläuft und parallel zum Durchmesser AB ist. Die Länge von EF beträgt 36 cm.

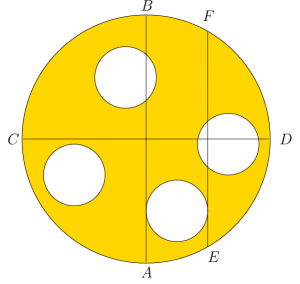
Abbildung 1: Der übrig gebliebene Teig.

Wie groß ist die Fläche des übrig gebliebenen Teigs?

Antwortmöglichkeiten

1. 244\pi cm^2
2. 300\pi cm^2
3. 312\pi cm^2
4. 320\pi cm^2
5. 324\pi cm^2
6. 344\pi cm^2
7. 360\pi cm^2
8. 368\pi cm^2
9. 381\pi cm^2
10. Es gibt nicht genügend Informationen, um die Fläche des übrig gebliebenen Teigs zu berechnen.