
Aufgabe
Der Weihnachtsmann ist derzeit damit beschäftigt, Geschenke für Kinder zu entwerfen. Jedes Geschenk sollte aus einer oder mehreren der n Arten von Süßigkeiten bestehen, die als S_1, \dots, S_n bezeichnet werden. Der Weihnachtsmann ist begeistert davon, für jedes Kind ein einzigartiges Geschenk zu schaffen und das Teilen von Süßigkeiten unter ihnen zu fördern. Um dies zu erreichen, hat der Weihnachtsmann um die Hilfe der Elfen gebeten.
Genauer gesagt sind die Elfen damit beauftragt, die maximale Anzahl M von Geschenken zu bestimmen, die als G_1, \dots , G_M bezeichnet werden, und die dann an M Kinder verteilt werden sollen, wobei jedes Kind genau ein Geschenk erhält. Die Geschenke werden durch die enthaltenen n Süßigkeiten S_1, \dots , S_n definiert und sollten die folgenden beiden Bedingungen erfüllen.
- Die Einzigartigkeit der Geschenke ist wesentlich, und der Weihnachtsmann möchte, dass alle Geschenke unterschiedlich sind. Zwei Geschenke G_i und G_j gelten als unterschiedlich, wenn eines davon eine Art von Süßigkeiten enthält, die das andere nicht enthält (obwohl sie einige Arten von Süßigkeiten teilen dürfen).
- Um das Teilen von Süßigkeiten unter den Kindern zu fördern, wünscht sich der Weihnachtsmann, dass jede Kombination von zwei Geschenken alle n Süßigkeiten S_1, . . . , S_n enthält. Auf diese Weise haben zwei Kinder, die sich entscheiden, ihre Geschenke zu kombinieren, Zugang zu allen Süßigkeiten.
Ein Beispiel für n=5 ist in der folgenden Abbildung dargestellt.
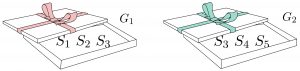
Für n=5 erfüllen die Geschenke G_1 und G_2 die Bedingungen (1) und (2).
Was ist die größte Anzahl M von Geschenken G_1, \dots , G_M, die die Elfen entwerfen können und die die Bedingungen (i) und (ii) erfüllen?
Anmerkung: Leere Geschenke zählen als Geschenke.
Antwortmöglichkeiten
- 3
- 4
- n
- n+1
- \frac{n(n-1)}{2}
- \frac{n(n-1)}{2} + 1
- n^2
- n^2+1
- 2^{n-1}
- 2^{n-1}+1