
© Friederike Hofmann, MATH+
Autor: Lukas Protz (MATH+)
Aufgabe
Zur Entlastung der Elfen bei der Färbung von Geschenkverpackungen, die in der Form eines Würfels sind, hat der eifrige Elf Eifi eine Maschine gekauft. Diese soll die Färbungen für die Elfen übernehmen. So eifrig wie Eifi ist, hat er auch schon alle Deckel für die Geschenkverpackungen mit der Maschine anfertigen lassen. Sie sind alle mit gelben Sternen auf dunkelblauem Hintergrund gefärbt.
Leider hat Eifi vergessen vorher den Weihnachtsmann zu fragen, ob die Elfen die Maschine überhaupt benutzten dürfen. Dieser ist nämlich nicht begeistert darüber, dass die Deckel der Geschenke alle gleich aussehen. Damit er beim Austeilen der Geschenke an Weihnachten möglichst schnell das richtige findet, hätte er am liebsten, dass alle Geschenke unterschiedlich aussehen. Auch findet er bunte Geschenke viel schöner als einfarbige.
Eifi versucht den Weihnachtsmann zu beruhigen. Dazu zeigt er ihm, dass die Maschine jede der übrigen fünf Seiten eines Geschenks zufällig färben kann. Für die Färbung stehen sogar neun unterschiedliche Farben zur Verfügung.
Der Weihnachtsmann ist davon jedoch nicht überzeugt. Es könnte trotzdem passieren, dass ein Geschenk nur in einer oder zwei Farben gefärbt wird. Daher macht er Eifi ein Angebot. Er soll zunächst bestimmen, wie viel unterschiedliche Färbungen der Verpackung ohne Deckel es mit den neun Farben gibt. Dabei sind zwei Geschenke unterschiedlich gefärbt, falls sie sich nicht nur durch Spiegelungen oder Drehungen voneinander unterscheiden. Sei a der Anteil aller Färbungen, bei denen die Anzahl der Seiten, die die gleiche Farbe wie eine andere Seite haben, höchstens zwei beträgt. Die Elfen dürfen die Maschine benutzen, wenn der Anteil a größer als 0,7 ist. Ansonsten müssen sie wie immer alle Geschenke selbst einfärben, damit immer alle Seiten eine unterschiedliche Farbe haben. Wie hoch ist der Anteil a der Geschenke mit höchstens zwei gleichfarbigen Seiten?



Abbildung 1: Ein bereits verpacktes Geschenk. oben links: Das Geschenk von einer Seite, oben rechts: Das gleiche Geschenk von der gegenüberliegenden Seite, unten: Der Netzplan der Geschenkverpackung ohne Deckel.
Erklärung von Spiegelung und Drehung
Um das Konzept der Spiegelung zu erklären, betrachten wir zwei 2\times 4 Gitter:
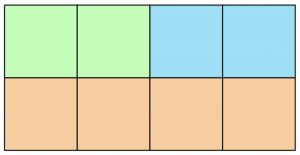
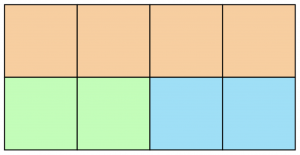
Diese Gitter sind nicht verschieden, da sie sich nur durch eine Spiegelung zwischen den beiden Reihen unterscheiden.
Um das Konzept der Drehung zu erklären, betrachten wir erneut zwei 2\times 4 Gitter:

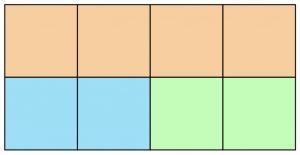
Diese Gitter sind nicht verschieden, da sie sich nur um eine Drehung mit Drehwinkel \pi (oder 180^\circ) unterscheiden.
Antwortmöglichkeiten
- a \le 0,1
- 0,1 < a \le 0,2
- 0,2 < a \le 0,3
- 0,3 < a \le 0,4
- 0,4 < a \le 0,5
- 0,5 < a \le 0,6
- 0,6 < a \le 0,7
- 0,7 < a \le 0,8
- 0,8 < a \le 0,9
- 0,9 < a