16 Das Schafhotel – Mathekalender

Autor: Matthew Maat (Universiteit Twente)

Projekt: Combining algorithms for parity games and linear programming

Aufgabe

Mit dem Klang des Engelschores noch in ihrer Erinnerung nachhallend, machen sich die Hirten Ananias, Benjamin, Caius und David auf den Weg nach Bethlehem. Zuvor müssen sie jedoch ihre Schafe in einem Schafhotel abgeben, da sie große Herden verschiedener Schafsarten haben. Alle vier gehen zu unterschiedlichen Hotels. Die Standardregeln für Schafhotels im ersten Jahrhundert lauten wie folgt:

Es dürfen so viele Zimmer benutzt werden, wie man möchte.
Es ist nicht erlaubt, zwei verschiedene Schafsarten über genau denselben Satz von Zimmern zu verteilen. Zum Beispiel, wenn alle schwarzen Schafe auf Zimmer 1 und 2 verteilt werden, können alle weißen Schafe in Zimmer 1 verweilen oder es können die weißen Schafe auf Zimmer 1, 2 und 3 aufgeteilt werden, aber die weißen Schafe dürfen nicht ebenfalls genau auf Zimmer 1 und 2 aufgeteilt werden. Ebenso ist es beispielsweise nicht erlaubt, alle schwarzen und alle weißen Schafe nur auf Raum 1 zu verteilen.
Für jede Schafsart $x$ und $y$ gibt es eine Art $z$ (die auch $x$ oder $y$ sein kann), sodass folgendes für jedes Zimmer gilt: Entweder gibt es keine Schafe der Art $x, y$ oder $z$ in diesem Zimmer, oder es gibt Schafe der Art $z$ in diesem Zimmer und auch Schafe der Art $x$ und/oder $y$ .
Der Preis wird durch das Zimmer mit den meisten Schafsarten bestimmt. Gezahlt werden so viele Goldstücke, wie es Schafsarten in diesem Zimmer gibt.

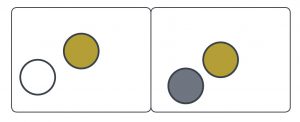
Als Beispiel betrachten wir einen Hirten mit schwarzen (s), weißen (w) und braunen (br) Schafen und erfüllen die Regeln wie folgt (vgl. Abb. 1):

Zu Regel 1: Der Hirte benutzt zwei Zimmer.
Zu Regel 2: Er platziert alle weißen Schafe in Zimmer 1, alle schwarzen Schafe in Zimmer 2 und teilt die braunen Schafe auf Zimmer 1 und 2 auf.
Zu Regel 3 (vgl. Tabelle in Abb. 1): Wenn $x$ für schwarze und $y$ für weiße Schafe steht, dann wählen wir für $z$ braune Schafe. (Vertauschen wir die Rollen von $x$ und $y$ so wählen wir trotzdem die gleiche Schafsart als $z$ . Nach dieser Konvention wird auch die Tabelle in Abb. 1 nur verkürzt dargestellt.) Wenn $x$ für schwarze oder weiße Schafe steht und $y$ für braune Schafe, dann wählen wir auch $z$ als braune Schafe.
Zu Regel 4: Das Zimmer mit den meisten Schafsarten enthält in diesem Fall zwei Schafsarten. Also bezahlt der Hirte zwei Gold.

$\begin{array}{|c|c|c|c|}\hline\textbf{x, y} & \mathrm{s}, \mathrm{w} & \mathrm{w}, \mathrm{br} & \mathrm{s}, \mathrm{br}\\\hline\textbf{z} & \mathrm{br} & \mathrm{br} & \mathrm{br}\\\hline\end{array}$

Abbildung 1: Die günstigste Aufteilung für einen Hirten mit 3 Schafsarten. Oben: Die Aufteilung auf die Räume. unten: Die dazugehörige Tabelle mit der Abbildung $x,y\mapsto z$ .

Nun ist bekannt, dass Ananias 4 Schafsarten hat, Benjamin 5, Caius 6 und David 7. Jeder Hirte findet aufgrund seiner Erfahrung mit den Regeln schnell die Verteilung der Schafe, die für ihn am wenigsten kostet. Es stellt sich heraus, dass jeder von ihnen nur 3 Zimmer für eine günstigste Aufteilung benötigt. Ananias zahlt $A$ Gold, Benjamin zahlt $B$ Gold, Caius zahlt $C$ Gold und David zahlt $D$ Gold. Was ist $A + B + C + D$ ?

Antwortmöglichkeiten

Aufgabe als PDF