
© Zyanya Santuario, MATH+
Autor: Matthew Maat (Universiteit Twente)
Projekt: Combining algorithms for parity games and linear programming
Aufgabe
Nach Rücksprache mit König Herodes machen sich die drei heiligen Könige bereit, von Jerusalem nach Bethlehem zu reisen. Allerdings gibt es ein Problem, das sie vor ihrer Abreise lösen müssen: Steuern. Aufgrund der großen Menge an Gold und Gewürzen, die sie mit sich führen, müssen sie in jeder Stadt, die sie betreten, Steuern zahlen. Um alles noch schlimmer zu machen, haben die cleveren Steuereintreiber alle Straßenschilder in Richtung der Orte gelenkt, an denen man die höchsten Steuern zahlen muss. Auf der Karte (Abb. 1) sind die Straßen und Städte zwischen Jerusalem und Bethlehem zu sehen. Die Straßen werden durch Pfeile und die Städte durch Kreise repräsentiert. Rote Pfeile markieren hierbei die Richtungen, in die die Schilder in der jeweiligen Stadt zeigen. In den Kreisen steht wie viel Steuern die heiligen drei Könige in jeder Stadt zahlen müssen.
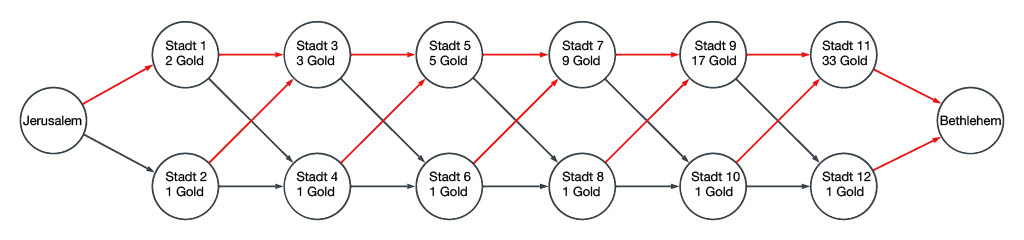
Abbildung 1: Die Straßen (Pfeile) von Jerusalem nach Bethlehem mit den Steuerbeträgen in den Kreisen. Güter können nur in Richtung der Pfeile transportiert werden.
Die drei heiligen Könige entscheiden sich, Balthasar mit folgendem Auftrag vorauszuschicken:
- Beginnend in Jerusalem, soll er zu Stadt 1 gehen, dann zu Stadt 2, 3 usw. Da Balthasar zu Fuß unterwegs ist, kann er alle vorhandenen Straßen ignorieren.
- Wenn Balthasar in einer Stadt ist, in der er das Schild so ändern kann, dass die Reise von dieser Stadt nach Bethlehem günstiger wird, ändert er das Schild, rennt zurück nach Jerusalem und beginnt den gesamten Prozess von vorne.
- Wenn Balthasar das Schild ändert, darf es nur in Richtung der Pfeile der Straßen zeigen. Zum Beispiel kann in Stadt 7 das Schild nur auf Stadt 9 oder Stadt 10 zeigen.
- Wenn Balthasar Bethlehem erreicht, schickt er eine Brieftaube, um den anderen mitzuteilen, dass sie nach Bethlehem kommen können.
Auf seiner ersten Reise ändert Balthasar das Schild in Jerusalem in Richtung Stadt 2, da dann die Gesamtsteuer für die Reise von Jerusalem aus 1 + 3 + 5 + 9 + 17 + 33 Goldstücke beträgt, anstelle von 2 + 3 + 5 + 9 + 17 + 33 Goldstücken. Auf seiner zweiten Reise ändert Balthasar das Schild in Stadt 1 in Richtung Stadt 4. Auf seiner dritten Reise ändert er das Schild in Jerusalem zurück nach Stadt 1. Das liegt daran, dass die Reise von dort nach Betlehem günstiger wird. Tatsächlich kostet die neue Reise 2 + 1 + 5 + 9 + 17 + 33, was günstiger ist als die Kosten von 1 + 3 + 5 + 9 + 17 + 33 der alten Reise.
Wie oft ändert Balthasar insgesamt ein Schild? (Wenn das Schild in einer Stadt mehrmals geändert wird, zählen wir es mehrmals.)
Antwortmöglichkeiten
- 55
- 57
- 63
- 83
- 114
- 120
- 126
- 177
- 240
- 367
Projektbezug
Der Algorithmus, den Balthasar verwendet, wird als der Strategy Improvement Algorithmus bezeichnet. Der Algorithmus nutzt eine sogenannte improvement rule, die festlegt, in welcher Reihenfolge Verbesserungen vorgenommen werden (oder in welcher Reihenfolge Balthasar die Städte besucht). In diesem Fall verwenden wir die sogenannte Bland-Regel. Obwohl es sich um ein Ein-Spieler-Spiel handelt (wir minimieren nur den Preis), können wir den Algorithmus auch verwenden, wenn es Städte gibt, die von einem Maximierer oder einem zufälligen Spieler kontrolliert werden. Es ist unbekannt, ob es eine improvement rule gibt, die eine geringe Anzahl von Iterationen garantiert. Wie man sehen kann, kann selbst bei einer kleinen Anzahl von Städten Blands Regel eine große Anzahl von Iterationen erfordern.