
© Ivana Martic, MATH+
Autor*innen: Ravi Snellenberg, Martin Skrodzki (TU Delft)
Projekt: Holonomy, Computer Graphics and Visualization
Aufgabe
Die Elfen des esoterischen Forschungsbereichs haben einen Weg gefunden, die Lagerkapazität im aktuellen Lagerraum zu erhöhen. Dies war dringend nötig aufgrund der ständig wachsenden Menge an Geschenken, die jedes Jahr gelagert werden müssen. Die Art und Weise, wie die Elfen dies erreicht haben, besteht darin, die Räume im aktuellen Lagerhaus auf clevere Weise mithilfe von Portalen zu verbinden. Normalerweise konnte man 4 quadratische Räume um eine Ecke platzieren, aber mit der Art und Weise, wie die Räume jetzt verbunden sind, müsste ein Elf durch 5 quadratische Räume gehen, um um den Eckpunkt zu laufen, an dem die Räume zusammentre ffen, anstatt der üblichen 4 (siehe Abb. 1). Aufgrund der Schwierigkeit, diese raumverändernden Portale zu erstellen, können die Elfen sie nur in einem begrenzten, separaten Bereich erstellen, der von Wänden umgeben ist. Dieser Bereich wird als Kontrollraum bezeichnet. Um das Lager zu durchqueren, betreten die Elfen also den Kontrollraum anstelle des physischen Lagers. Und wenn ein Elf in ein anderes Quadrat im Kontrollraum geht, betritt er einen neuen Lagerraum. Welcher Raum dies ist, wird durch die neue Art der Verbindung der Räume entschieden. Der Kontrollraum ist ein Raster von 3\times 3 Räumen mit Portalen an jeder Wand, die zwei quadratische Räume innerhalb des Kontrollraums trennen (siehe Abb. 1). Ecken haben keine Portale, sodass es nicht möglich ist, diagonal im Kontrollraum zu gehen, sondern nur orthogonal. Trotz dieser Einschränkung ist es immer noch möglich, jeden der möglicherweise unendlichen Räume im Lager zu erreichen, indem man die Anordnung der Räume auf clevere Weise nutzt.
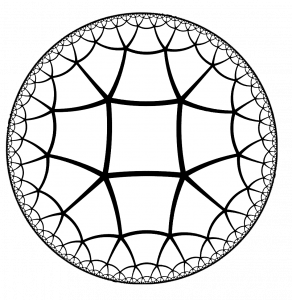

Abbildung 1: Das Lagerraum-Layout. Die linke Abbildung zeigt eine Karte des neuen Lagerlayouts. Jedes Viereck ist tatsächlich ein quadratischer Raum, obwohl sie auf der Karte verzerrt erscheinen. Dies ist aufgrund der Notwendigkeit, den zusätzlichen fünften Raum an jeder Ecke darzustellen. Es wird das Poincaré-Kreisscheibenmodell verwendet, um dieses spezielle Layout anzuzeigen. Die rechte Abbildung zeigt den Kontrollraum.
Da die Elfen im esoterischen Forschungsbereich erkannten, dass die gesamte Situation wirklich verwirrend ist, haben sie eine Infografik erstellt, die sie an die Vordertür des Kontrollraums hängten, siehe Abbildung 2.
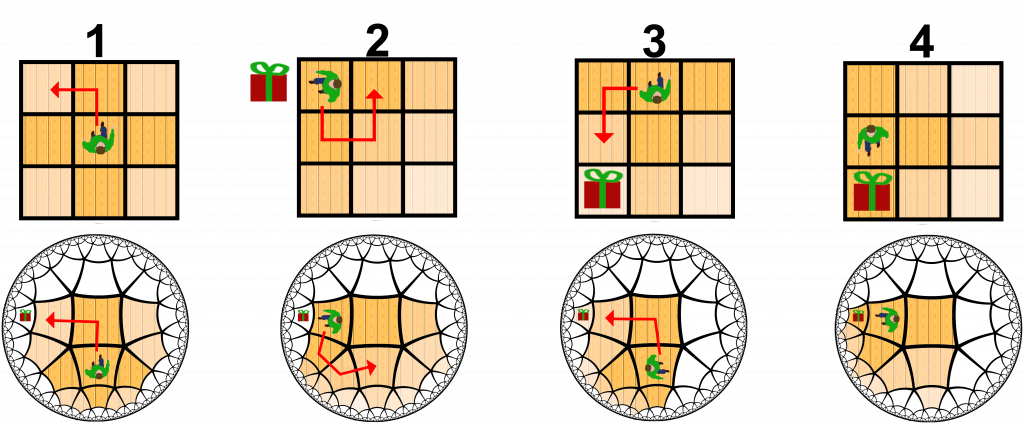
Abbildung 2: Die Infografik. Je heller der Boden wird, desto weiter entfernt ist ein Raum.
Die Infografik zeigt eine hypothetische Situation, in der ein Elf ein Geschenk erreichen muss, das nicht direkt erreichbar ist, basierend auf dem Ausgangslayout des Kontrollraums. Der obere Teil der Infografik zeigt den Kontrollraum, in dem sich der Elf bewegt, während er durch das Lager geht. Der untere Teil der Infografik zeigt eine Draufsicht auf das Lagerlayout, das mit der darüber liegenden Ansicht des Kontrollraums verknüpft ist. Die farbigen Räume in der Infografik sind die Räume, die durch Gehen eines direkten Pfades (eines kürzesten Pfades) zu einem Raum im Kontrollraum von der aktuellen Position des Elfen aus erreichbar sind. Das Gehen unterschiedlicher kürzester Pfade zum gleichen Raum im Kontrollraum führt nicht immer zum gleichen Raum im Lager. Zum Beispiel kann der Elf im Kontrollraum, der im ersten Schritt der Infografik angezeigt wird, jeden Eckraum auf zwei verschiedene Arten erreichen. Im Lagerlayout ist zum Beispiel zu sehen, dass beide Arten, die obere rechte Eckenkachel im Kontrollraum zu erreichen (erst nach oben, dann nach rechts oder erst nach rechts, dann nach oben), zu zwei verschiedenen Räumen im Lager führen, siehe Abb. 3.
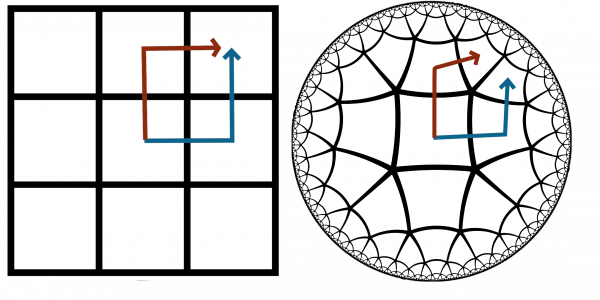
Abbildung 3: Links: Zwei Wege zur oberen rechten Ecke im Kontrollraum. Rechts: Die entsprechenden Wege im tatsächlichen Lager.
Die Infografik zeigt, dass es durch Gehen im Kontrollraum auf bestimmte Weise möglich ist, das Geschenk zu erreichen, obwohl es von der Ausgangsposition aus nicht direkt erreichbar war. Sie zeigt auch, wie sich der direkt zugängliche Bereich verschiebt, während der Elf durch das Lager geht.
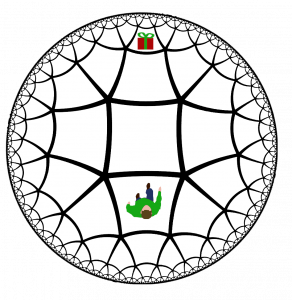
Jetzt fragen sich die entwicklungsorientierten Elfen des esoterischen Forschungsbereichs: Was ist die minimale Anzahl von Portalen, die durchquert werden müssen, um das Geschenk in der Situation von Abbildung 4 zu erreichen? Dieses wäre ohne die Beschränkung der Kontrollraumgröße in drei Schritten nach vorne erreichbar. Angenommen wird bei dem Szenario, dass der Elf in der Mitte des Kontrollraums startet.
Antwortmöglichkeiten
- 3
- 5
- 6
- 7
- 8
- 9
- 10
- 12
- 14
- 42
Projektbezug:
Das Szenario, das dieses Problem beschreibt, ist die Umgebung einer Virtual-Reality-Anwendung namens Holonomy (benannt nach der mathematischen Eigenschaft, die diese Durchquerung ermöglicht). Holonomy wird entwickelt, um verschiedene Fragen zu beantworten. Zum Beispiel Fragen wie
”Könnte eine solche Demonstration Menschen helfen, die zugrunde liegenden mathematischen Eigenschaften intuitiver zu verstehen?“, ”Wie schnell passen sich Menschen an die Navigation in einer hyperbolischen Welt an?“ und ”Wie könnten wir dem Spieler helfen, sich in einer solchen Umgebung zu bewegen?“. Und
wenn wir herausfinden können, wie man die Navigation in diesen hyperbolischen Räumen einfach gestalten kann, könnte es verwendet werden, um konsistente Welten jeder Größe zu schaffen, die in einem begrenzten Raum durchquert werden können. Das Berechnen der kürzesten Wege zwischen zwei Orten ist ein Beispiel für eine der Herausforderungen, die wir beim Erstellen von Holonomy entdeckt haben.