09 Geheime Geschenke

© Christoph Graczyk, MATH+

Autoren:  Felix und Nathanael Höfling

Projekt: EF 4-10

Aufgabe

Der Weihnachtsmann ist wie jedes Jahr sehr dankbar für die großartige Arbeit seiner Wichtel und möchte jeden von ihnen auch gern beschenken. Doch er kann die Namen nicht auf die Geschenke schreiben, da die Überraschung sonst nicht gelingt.

Eines Tages kommt Zwerg Alwin zu Besuch, und der Weihnachtsmann schildert ihm das Problem. “Lieber Alwin, was soll ich nur machen?” Der schlaue Alwin hat sofort eine Idee: “Du könntest für jeden Wichtel einen Geheimcode auf sein Geschenk schreiben. Es ist wichtig, dass kein Code doppelt vorkommt. Außerdem sollen ähnliche Namen ganz verschiedene Codes bekommen, damit sie die Namen nicht erraten können. Ich erstelle Dir gleich eine Liste mit den Codes.”

Für jedem Namen berechnet Zwerg Alwin auf folgende Weise einen vierstelligen Geheimcode:

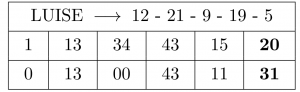
Zuerst übersetzt er die Buchstaben des Namens entsprechend ihrer Position im Alphabet in Zahlen, ein E wird eine 5, ein M eine 13, und das Z bekommt die 26 usw. Dann befüllt er eine Tabelle mit zwei Zeilen, siehe Tabelle unten. In die erste Spalte schreibt er oben eine 1 und unten eine 0. Dann addiert er in der ersten Zeile zu der zuletzt geschriebenen Zahl immer den Wert des nächsten Buchstabens hinzu. Bevor er das Ergebnis zu der Zeile hinzufügt, achtet er jedoch darauf, dass die Zahl kleiner ist als 47. Falls das Ergebnis größer oder gleich 47 ist, subtrahiert er 47 von dem Ergebnis. Ist das Ergebnis kleiner als 10, wird eine Null vorangestellt, z.B. aus 7 wird 07. In der zweiten Zeile geht er genauso vor, außer dass er zu der zuletzt geschriebenen Zahl immer den entsprechenden (oben drüber) Eintrag aus der ersten Zeile dazu addiert. Zuletzt nimmt er die jeweils letzte Zahl aus den beiden Zeilen und schreibt sie hintereinander, die Zahl aus der zweiten Zeile zuerst — dies ist der Geheimcode des Namens. Nach dieser Methode bekommt beispielsweise Luise den Code 3120, so wie es im Bild gezeigt ist.

Eine Weile später hält der Weihnachtsmann glücklich die Liste mit den Geheimcodes in der Hand und macht sich an die Arbeit. In der Wichtelwerkstatt bestellt er für jeden seiner Wichtel ein schönes Geschenk, doch nicht auf dessen Namen, sondern zu dem Geheimcode. Am Tag vor Heiligabend bereitet er seinen Schlitten vor.

Am Nordpol ist es kalt und es wütet ein fürchterlicher Schneesturm. Als sich der Weihnachtsmann zu seinen Rentieren umdreht, öffnet sich sein Mantel etwas, der Wind erfasst die Liste mit den Geheimcodes und weht sie davon. Der Weihnachtsmann ist schockiert.

Zurück in der Wichtelwerkstatt nimmt er das erste Geschenk in die Hand. Es hat die Aufschrift “2122”. Doch welchem Wichtel soll er es geben? Kannst Du ihm helfen? Für wen ist das Geschenk?

Antwortmöglichkeiten

1. Lotte
2. Flavia
3. Luiz
4. Elisabeth
5. Nathanael
6. Matteo
7. Evelina
8. Mathilda
9. Lutz
10. Fridolin

Projektbezug

Zur Modellierung kooperativen Verhaltens werden häufig agentenbasierte Modelle eingesetzt. Diese Modelle beschreiben Zehntausende unabhängig agierender Einheiten (Personen, Tiere, Autos, Mobiltelefone, ...), die jedoch miteinander im Austausch stehen. Dadurch können unter anderem großräumige Strukturen entstehen, die sich mit wenigen Parametern beschreiben lassen, beispielsweise Grüppchenbildung oder Cluster. Die enorme Informationsfülle des ursprünglichen Modells lässt sich also auf wenige wichtige Kennzahlen reduzieren. Umgekehrt kann man aus den Kennzahlen kaum mehr auf die Positionen der einzelnen Agenten schließen. Wie solche Zusammenhänge mathematisch formuliert und berechnet werden können, ist Gegenstand der aktuellen Forschung.

Ganz ähnlich reduzieren wir in der Aufgabe lange und kurze Namen stets auf dieselbe Länge. Die Umkehrung der Abbildung, also die Berechnung des Namens anhand des Codes ist nahezu unmöglich. Anders als bei den Agentensystemen haben die Codes zusätzlich die Eigenschaft, dass ähnlichen Namen deutlich verschiedene Codes zugeordnet werden. Somit fungiert der Code auch als Prüfsumme, damit lassen sich dann Buchstabendreher entdecken. Es gibt noch viele andere Anwendungen solcher Codes, beispielsweise das sichere Überprüfen von Passwörtern auf einem Computer, ohne dafür das eigentliche Passwort speichern zu müssen.

Zur mathematischen Konstruktion der Codes: die Berechnung geschieht in Anlehnung an die Adler32–Hash–Funktion.