
© Ivana Martic, MATH+
Autor*innen: EWM-NL
Aufgabe
Julia Robinson war eine der besten Mathematikerinnen des 20. Jahrhunderts und ist eine alte Freundin des Weihnachtsmanns. Sie hat an dem sogenannten 10. Hilbert-Problem gearbeitet, aber auch im Bereich der Spieltheorie geforscht. Jetzt braucht der Weihnachtsmann ihre Hilfe bei einem lustigen Spiel, das seine Elfen entwickelt haben, um sich beim Arbeiten an einem Förderband zu amüsieren.
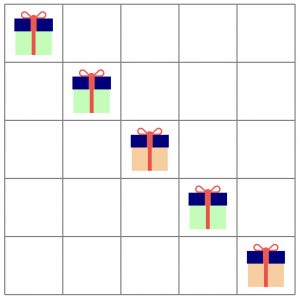
Abbildung 1: Der Fertigungsprozess für n = 5.
Der Weihnachtsmann verpackt und versendet Geschenke mit n Förderbändern. Der Fertigungsprozess ist ein n\times n Quadratgitter, und alle n Pakete befinden sich auf der Diagonalen dieses Quadrats, siehe Abbildung 1. Um sie verschicken zu können, müssen diese Pakete in die unterste Reihe des Quadrats transportiert werden. Dazu können die Elfen des Weihnachtsmanns die Geschenke nach unten bewegen. Sie können dies jedoch nur tun, indem sie gleichzeitig zwei Pakete um einen Schritt nach unten bewegen. Pakete in der untersten Reihe können nicht weiter bewegt werden, da sie sonst von den Förderbändern fallen würden.
Der Weihnachtsmann möchte, dass die unterste Reihe mit allen n Geschenken gefüllt ist (damit alle Pakete verschickt werden können). Manchmal scheinen seine Elfen jedoch stecken zu bleiben und können nicht alle Geschenke versenden. Wann ist es möglich, dass der Weihnachtsmann alle Geschenke mit einem Algorithmus bis zum unteren Ende des Quadrats bringen kann, ohne stecken zu bleiben?
Antwortmöglichkeiten:
- Für jeden Wert von n.
- Wenn n gerade ist.
- Wenn n ungerade ist.
- Für alle n \ge 24.
- Für alle n \ge 12.
- Für alle n, bei denen entweder n-1 oder n ein Vielfaches von 4 ist.
- Für alle n, bei denen entweder n+1 oder n ein Vielfaches von 4 ist.
- Für alle n, bei denen entweder n-1 oder n ein Vielfaches von 3 ist.
- Für alle n, bei denen entweder n+1 oder n ein Vielfaches von 3 ist.
- Für keinen Wert von n.
Projektbezug:
EWM-NL ist der niederländische Verband für Frauen in der Mathematik.