
© Julia Nurit Schönnagel, MATH+
Author: Dante Luber (BMS, Goethe University Frankfurt)
Challenge
The elves, who are diligently packing gifts for Santa, want to play football in their free time. They have repeatedly asked Santa for a football, but due to this year’s tight budget, he refuses to buy one. A clever elf named Mo, who makes gift boxes, has the brilliant idea of crafting the football himself. Mo has access to a machine that can print various body nets (2D shapes) onto sturdy paper. However, Mo is unsure which net to print so that it can be folded and glued into a ball. So, he asks the smart elf Mara for advice.
Mara responds: “I can’t guarantee a design that will result in a perfect ball, but I know of a cool object that you can use for the game.”
She shows Mo a picture of the body they can craft for the game (see Figure 1).
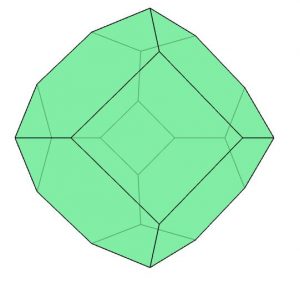
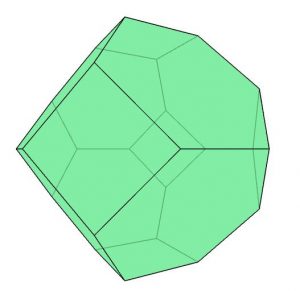
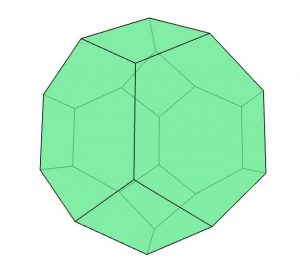
Figure 1: Three 3D images of the final football from different angles
Excited, Mo asks Mara for the design of the pattern. Mara goes to the office and searches her computer for the file containing the net for this body. Unfortunately, she can’t remember which number the design has. However, she is sure that it is among these 8 designs and prints all 8 possible nets. Mo must figure out which of the nets shown below corresponds to the object in Figure 1. Which net (1) through (8) must Mo choose to fold it into this object?
The nets are shown in the PDf and will come here soon! 🙂

Net 1
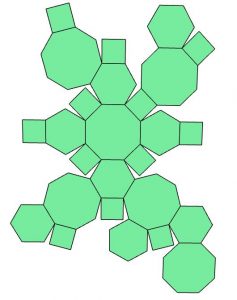
Net 2
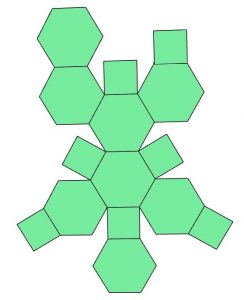
Net 3
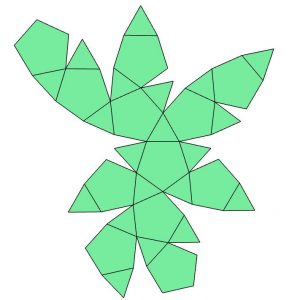
Net 4
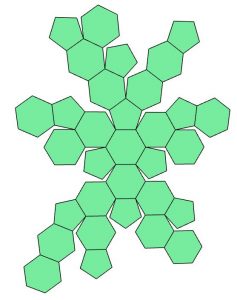
Net 5
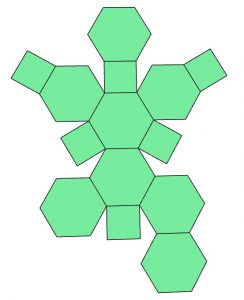
Net 6
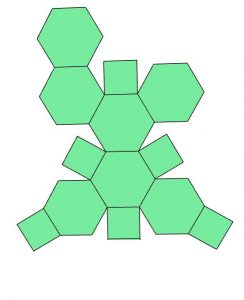
Net 7

Net 8
Possible Answers
- Net 1
- Net 2
- Net 3
- Net 4
- Net 5
- Net 6
- Net 7
- Net 8
- All
- None
Project Reference
- The figures were generated using OSCAR —Open Source Computer Algebra Research System, Version 1.0.0, developed by The OSCAR Team, 2024.
- The OSCAR project is developed within the TRR 195 into a visionary next generation open source computer algebra system surpassing the combined mathematical capabilities of the underlying systems.
- OSCAR allows users to construct new mathematical objects efficiently by combining existing building blocks from any of the cornerstones and equip these objects with mathematical capabilities exceeding those of the individual systems in a transparent way.
- For more information, or if you want to use Oscar yourself, visit https://www.oscar-system.org.
- This challenge was inspired by MatchTheNet, a free, online, polyhedral geometry game developed by the polymake team. You can play the full game at https://www.matchthenet.de/