
© Ivana, Martić MATH+
Author: Christian Haase
Project: AA3-12
Challenge
The elves are creating gift cards from graph paper, which they usually use for calculations, for the children in a variety of shapes. To make production easier, Santa has required that all cards take the form of a closed convex polygon, and all vertices of that polygon are graph-paper crossing points.
Here, “convex” means that you can walk along the path making only right turns, and “vertices” means points where the elf has to change directions while cutting the paper, which restricts certain shapes from being used:
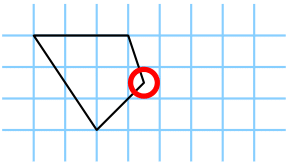
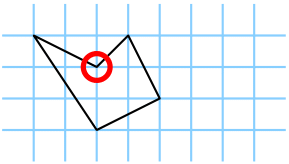
Figrue 1: Examples for one allowed (left) and one forbidden card (right)
The first picture in Figure 1 shows a convex card where a vertex is not a graph-paper crossing point, and the second picture shows an example of a non-convex card. Santa denotes by b the number of graph-paper crossing points along the boundary of the card, and by i the number of graph-paper crossing points inside of the card.
Santa also wants to conserve paper, so he requires that each card has a specific area. For each such polygon, the enclosed area is denoted by a , where the side length of a square of the graph-paper is 1 decimeter.
For instance, a gift card with 3 boundary graph-paper crossing points, zero interior graph-paper crossing points, and an area of 0.5 would have the shorthand notation \left( 3, 0, \frac{1}{2} \right) , as shown in Figure 2 (a). Similarly, a gift card with values (9, 1, 4.5) can be observed in Figure 2 (b).
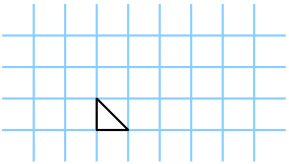
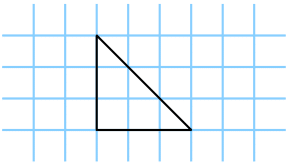
Figure 2: Example of two valid cards
The elves are now worried that some gift cards may no longer be possible to create. Which of the following triples (b, i, a) can they still create?
- (24, 16, 27)
- (15, 7, 13.5)
- (3, 9, 9.5)
- (18, 0, 9)
Possible Answers
- (yes, yes, yes, yes)
- (yes, yes,no, yes)
- (yes, yes,yes, no)
- (yes, no,yes, yes)
- (no, yes,yes, yes)
- (no,yes,no, yes)
- (yes, no, yes, no)
- (no,no,yes, yes)
- (no,no,no, yes)
- (no,no,no, no)
Projekt Reference
The project aims to deepen our understanding of the expressivity of neural networks (NNs). Specifically, it establishes both lower and upper bounds on the topological simplification that a ReLU neural network can achieve given a particular architecture.
In the context of general representations of functions, we observe that the function computed by a ReLU NN is piecewise linear and continuous (CPWL) since it is a composition of affine transformations and the ReLU
function. Conversely, it is known that any CPWL function can be represented by a ReLU NN of logarithmic depth. In [1] it has been conjectured that this logarithmic bound is tight. In other words, there may exist CPWL functions that can only be represented by ReLU NNs with logarithmic depth. This conjecture has been proven under a natural assumption for dimension n=4 using techniques from mixed-integer optimization. Additionally, in [2] it has been shown that logarithmic depth is necessary to compute the maximum of n numbers when only integer weights are allowed. This result is based on the duality between neural networks and Newton polytopes through tropical geometry. One of the primary goals of this project is to either prove or disprove the conjecture in its full generality.
[1] Christoph Hertrich, Amitabh Basu, Marco Di Summa, and Martin Skutella.
Towards lower bounds on the depth of ReLU neural networks.
SIAM Journal on Discrete Mathematics, 37(2):997–1029, 2023.
[2] Christian Haase, Christoph Hertrich, and Georg Loho.
Lower bounds on the depth of integral ReLU neural networks via lattice polytopes, 2023.