16 The Numbers of Nazareth

© Zyanya Santuario, MATH+

Author: Matthew Maat (Unversiteit Twente)
Project: Combining algorithms for parity games and linear programming

Challenge

In the tiny village of Nazareth, which you see in Figure 1(i), there are only six streets. It is possible to walk a cycle, which means you walk along a number of streets, and you return to where you started (without passing a crossing twice). For example the roads a, d and f form a cycle. We denote this cycle as (adf). In total there are seven cycles, the other ones are (bde), (cef), (abc), (adec), (abef) and (bcfd). Note, that the starting position of a cycle does not matter, e.g. the cycles (adf) and (dfa) are regarded as the same cycle.

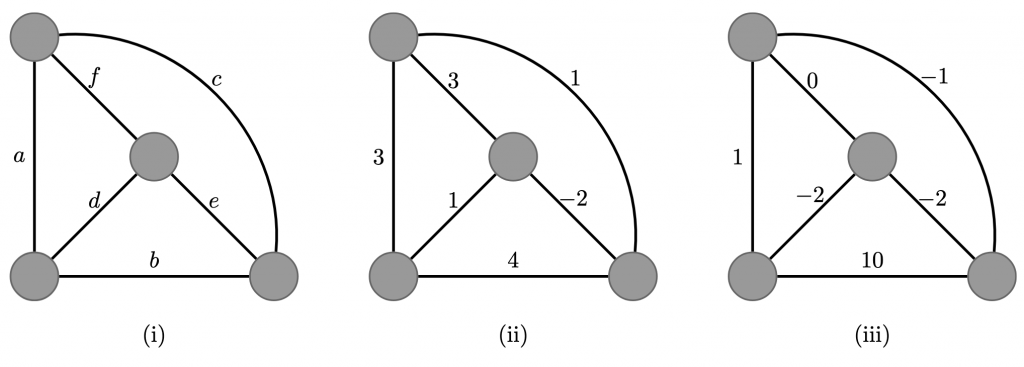
Figure 1: The streets of Nazareth

Now Joseph and Mary are playing a game called `number the streets.’ Each round starts with the village elder revealing a set of cycles, for example he gives them (bde),(abc), (bcfd) and (abef). Mary and Jpseph have a map of the village. They each write down six integers on the map, one on every street in the map.

Joseph gets one point if both of these are true:

• In each cycle that the elder gave, the largest integer that Joseph wrote is even.
• In every other cycle, the largest integer that Joseph wrote is odd.

Mary gets one point if both of these are true:

• In each cycle that the elder gave, the sum of the integers that Mary wrote is at least 0.
• In every other cycle, the sum of the integers that Mary wrote is less than 0.

Joseph and Mary play a practice round:
Figure 1 shows the numbers written by Joseph (ii) and Mary (iii) to score a point in the round where the eldest would have announced the roads (bde), (abc), (bcfd), and (abef).
In the cycle (bde), which is part of the set, the highest number is 4, which is indeed even, and one can check that the two properties also hold for the other six cycles.
For Maria, the sum of the numbers in cycle (bde) is 10-2-2=6, which is even bigger than 0. And again, one can check that the other six cycles are also correct.

In the actual game, three rounds are played. After each round, Joseph and Mary cross out their old numbers and think of new numbers for the next round. The points scored are added up. The elder gives the following sets of cycles:

• Round 1: (adf) and (cef)
• Round 2: (abc), (bde), (cef) and (adf)
• Round 3: (abef) and (bcfd)

Assume Joseph and Mary play as optimally as possible. Let J be the total score of Joseph and M that of Mary. What is the final score, written as J-M?

Update: December 16, 4:35 pm, Possible Answer 5 changed

Possible Answers

1. 0-3
2. 1-3
3. 1-1
4. 1-2
5. 3-3
6. 2-1
7. 2-2
8. 2-3
9. 3-0
10. 3-1

PDF Latest Update: December 16, 4:45 pm, Corrected an error in possible anwer 5