13 Surrounded by Rubies

© Julia Nurit Schönnagel, MATH+

Author: Matthew Maat (Universiteit Twente)
Project: Combining algorithms for parity games and linear programming

Challenge

Somewhere in the Far East, the wise men are packing their gifts to present to the newborn king. As they are loading them into their camel bags, they realize that one of the cube-shaped boxes, which is decorated with rubies at some of its corners, is broken (Figure 1, left).

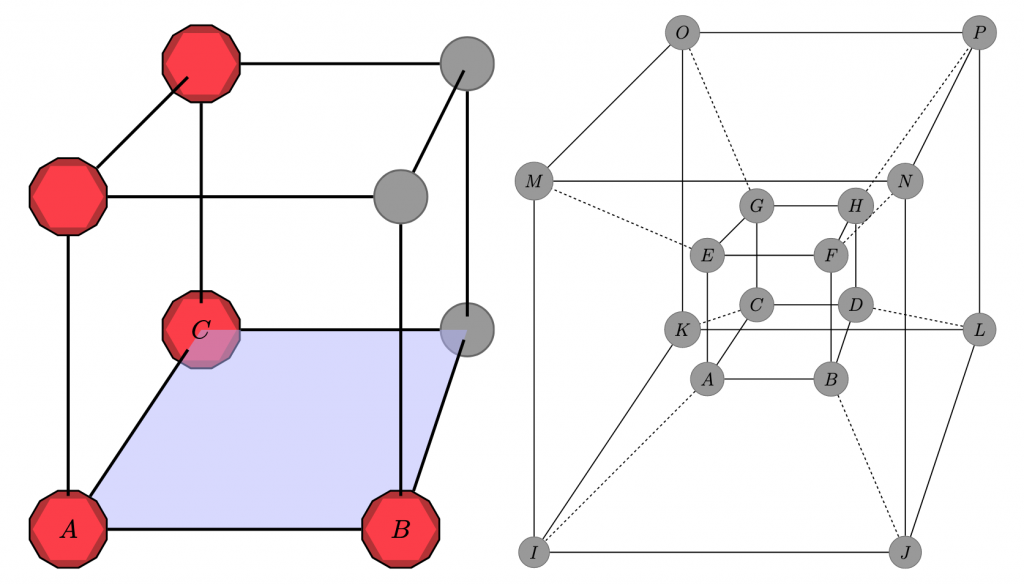
Figure 1: Left: original design of the (now broken) box. The rubies are colored in red. Right: the structure of a tesseract.

The ruby marked with A had fallen off. They can spot the hole in the design quickly because of an ancient eastern decoration pattern, where the rubies on the cube-shaped box are always placed in such a way that

• all the rubies are connected by edges
• the corners with no rubies, called non-rubies, are all connected by edges.
• And the same holds for every square (face of the box), i.e. all rubies in a square and all non-rubies are connected via edges.

In the blue square on this broken box, ruby B is now not connected to ruby C, so they see that the box must be broken.
While the wise men agree that the old box had a nice way of detecting if it is broken, it is not perfect: for example, if ruby B had fallen off instead of ruby A, you would not be able to detect it using the rules. So instead of repairing the old box, they want to make a new box. This time they want to use a so-called tesseract (a 4-dimensional hypercube, see description at the end of the challenge).
They want some corners of the tesseract to have rubies as well and have the following requirements for the design:

1. There is at least one ruby in the design.
2. All the rubies are connected with each other via some sequence of edges of the tesseract, and all non-ruby corners are also connected with each other by the edges of the tesseract.
3. In every cube in the tesseract, the same holds: all the rubies are connected, and all the non-rubies are connected.
4. In every square, also all the rubies are connected, and the non-rubies are connected
5. You can easily detect if one ruby goes missing: if any ruby disappears, there will be a square in which the rubies are not connected (in the same way as the blue square in Figure 1 left if ruby A disappears). Note, that we also consider the rubies connected, if there is no ruby on a square.

The wise men think for a long time, and find a design that meets not only the requirements, but also has the most rubies among all other designs meeting the requirements.

Question: How many rubies are placed on the tesseract in their design?

About the tesseract: In the same way that you can create a cube by taking two squares and connecting their four corners with edges, you can create a tesseract (in four dimensions) by taking two cubes and connecting the eight pairs of corners of the cubes (see Figure 1 right). A tesseract has 16 corners (A,B,C, \ldots, P), 32 edges (for example, edges AB,~JN and CK), 24 squares (like ABDC,~IKOM or JBFN), and 8 cubes (for example, A,B,C,D,E,F,G,H form a cube, and A,B,E,F,I,J,M,N form a cube). Since the tesseract is four-dimensional, the illustration 1 on the right is merely a projection. Consequently, squares or even cubes may appear distorted in the illustration.

Possible Answers

1. 4 or less rubies
2. 5 rubies
3. 6 rubies
4. 7 rubies
5. 8 rubies
6. 9 rubies
7. 10 rubies
8. 11 rubies
9. 12 rubies
10. 13 or more rubies