12 Cable Chaos

© Julia Nurit Schönnagel, MATH+

Author: Lukas Protz (TU Berlin, MATH+)

Challenge

Paula and Quentin are the head elves of the IT department at the North Pole. Usually, everything in the department goes according to plan, but one day they receive messages from two of the elves working there. They complain about having issues connecting to the winternet (the analog of the internet at the North Pole).

As the connection to the winternet is done with cables, Paula and Quentin think that some of the cables might be damaged, so they go to the cable room checking them. The cable terminals that correspond to the two elves are labeled “\frac{22}{7}” and “\frac{87}{32}“. Note that, despite the labels of the cables being in the form of fractions, they are just labels and (a priori) have no connection to rational numbers.

Once inside the cable room, Paula and Quentin get overwhelmed by a huge cable harness. How on earth should they find the two cable terminals they are searching for? Luckily, they find a note and a picture (compare Figure 1) on the wall explaining the labeling system of the cable terminals:

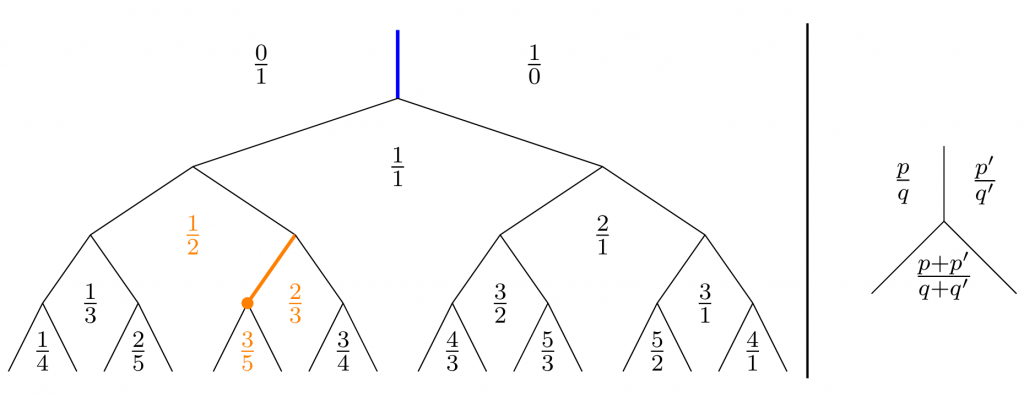
Figure 1: Left: The roots of the tree with the corresponding labels.
Right: The rule to obtain a new label if a root splits and one cable ends. The orange dot denotes the end of the cable labeled “\frac{3}{5}“.

1. The cables are arranged in a tree structure (the harness), see Figure 1. The cable bundles are the individual roots (edges) of the harness. There is one main root of the tree, colored blue in Figure 1.
2. The region to the left of the main root is labeled “\frac{0}{1}“, and the region to the right is labeled “\frac{1}{0}“.
3. Each time a root splits into two new roots, one cable ends and the others continue along one of the two new roots. The main root splits into two new roots. The cable that ends at this splitting point has the label “\frac{1}{1}“, which is obtained by combining the labels of the left and right region in the following way:

   \frac{0 + 1}{1 + 0} = \frac{1}{1}.

   The newly created region by the two new roots is also labeled “\frac{1}{1}“.

4. This process continues indefinitely. Each root splits into two new roots, one cable ends and a new region is created. If the labels of the right and left region of the root before the splitting point are “\frac{p}{q}” and “\frac{p'}{q'}“, then the cable that ends and the new region are labeled “\frac{p''}{q''}“, according to the following rule:

   \frac{p''}{q''} = \frac{p + p'}{q + q'}.

5. For example, the labels of the regions to the left and right of the root highlighted in orange in Figure 1 are “\frac{1}{2}” and “\frac{2}{3}” and the label of the new region and ending cable at the orange dot is

   \frac{1 + 2}{2 + 3} = \frac{3}{5}.

Now to find the cables in question, Paula and Quentin start from the main root. Each time a root splits, they continue following either the left or the right roots until they arrive at a splitting point for one of the searched cables. Can you help Paula and Quentin find the ends of the cables labeled “\frac{22}{7}” and “\frac{87}{32}” by determining the sum of right turns of Paula and Quentin and the sum of left turns of Paula and Quentin?

Example: To get from the main root to the splitting point where the cable labeled “\frac{3}{5}” is, they have to first turn left, then right, and finally left again.

Remark: To clarify our terminology around left and right regions, we define these concepts with respect to the main root. Define the distance of a splitting point from the main root as the number of splitting points along the path from the main root to that splitting point, moving through intermediate roots in the harness. For example, the splitting point labeled “\frac{1}{2}” has a distance of 2 from the main root.

A splitting point is said to be closer to the main root than another if its distance to the main root is less than that of the other point.

Each root connects two splitting points, one of which is closer to the main root. When traversing from the splitting point that is farther from the main root to the one that is closer, the left region is defined as the region in the direction of a 90^\circ counterclockwise rotation from the traversal direction, while the right region is in the direction of a 90^\circ clockwise rotation. The left root now is the new root at a splitting point that touches the left region. Similarly, the right root is the new root that touches the right region.

Possible Answers

1. 6 left and 8 right turns
2. 11 left and 8 right turns
3. 8 left and 9 right turns
4. 10 left and 9 right turns
5. 7 left and 10 right turns
6. 9 left and 10 right turns
7. 8 left and 11 right turns
8. 7 left and 12 right turns
9. 6 left and 13 right turns
10. Not both labels appear in the tree.