22 Lights out

©Vira Raichenko, MATH+

Author: Nikola Sadovek (FU Berlin)
Project: MATH+

Challenge

The elves have been very busy in their workshops making and packing all the gifts. Now it is time to deliver them from the workshops to Santa’s house on a sleigh so that he can later distribute them to the children.

Since their work at the workshops is done, it is time for the elves to turn off the lights before closing. The lighting system in each workshop consists of n \ge 7 light bulbs aligned in a row, numbered from 1 to n from left to right. Each light bulb can be in one of two states: turned on or turned off.

Due to a technical error, when the switch on lightbulb k is pressed, in addition to changing the state of that bulb (turned off becomes turned on, and vice versa), the state of the three light bulbs directly to the left of it (numbered by those indices k-3, k-2, k-1which are greater than zero) and the three light bulbs directly to the right to it (numbered by those indices k+1, k+2 and k+3 which are at most n) are all changed.For example, if the switch on light bulb k=2 is pressed, only the states of the lamps 1,2,3,4 and 5 are changed. See Figure 1 for an illustration.

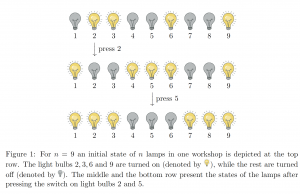
The elves would like to turn off all the light bulbs in every workshop using a sequence of such moves. For which values of n \ge 7 can the elves surely do that (i.e. for every initial state of the n light bulbs, there is such a sequence)?

Possible Answers

1. Exactly for those values of n \ge 7 which have residue 2 or 3 when divided by 7.
2. Exactly for those values of n \ge 7 which have residue 4 or 6 when divided by 7.
3. Exactly for those values of n \ge 7 which have residue 0 or 2 when divided by 7.
4. Exactly for those values of n \ge 7 which have residue 2 or 4 when divided by 7.
5. Exactly for those values of n \ge 7 which have residue 1 or 4 when divided by 7.
6. Exactly for those values of n \ge 7 which have residue 3 or 5 when divided by 7.
7. Exactly for those values of n \ge 7 which have residue 1 or 3 when divided by 7.
8. Exactly for those values of n \ge 7 which have residue 0 or 1 when divided by 7.
9. Exactly for those values of n \ge 7 which have residue 0 or 3 when divided by 7.
10. Exactly for those values of n \ge 7 which have residue 5 or 6 when divided by 7.