Skip to content

04 Christmas Chaos

©Vira Raichenko, MATH+

Author: Marieke Heidema (University of Groningen)

Challenge

Before Christmas, Santa’s elves are always working hard on Christmas presents for children from all around the world: they read the wish-lists and letters, make presents, and wrap the gifts, before sorting them and putting them in Santa’s sled.

In the days close to Christmas Eve, all the elves are working especially hard. This is also when there is a lot of chaos in Santa’s workshop: you will find elves frantically running over all the bridges connecting the different parts of Santa’s workshop, leaving behind a trail of ribbons and jumping over the rolls of wrapping paper that are covering the floor…

Last year, the elves made such a mess of the warehouse that Santa tripped and fell down, almost injuring himself, as he was inspecting the progress of the elves! This year, the elves want to make sure that Santa does not fall again. That is why the elves decided to clean up all the bridges connecting the 5 stations of the workshop:

(A)  the letter reading room

(B)  the gift factory

(C)  the gift-wrapping room

(D)  the sorting room

(E)  the warehouse with Santa’s sled

Their goal is to ensure a smooth and safe passage for Santa as he oversees their festive preparations. The layout of Santa’s workshop is as follows:

Figure-Heidema-Christmas_Chaos

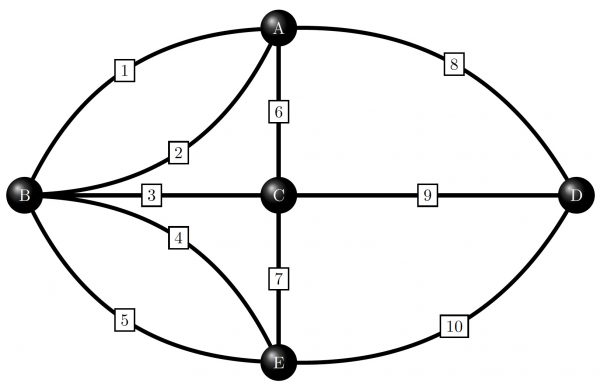
Here, the lines 1,2,…,10 each denote a bridge connecting the five different stations A,B,…,E of the workshop. Santa will make his round through the entire workshop and the elves need to know what path they have to follow to clean all the bridges efficiently before Santa comes. The two important questions are:

1. Is it feasible to tidy up the workshop while traversing each bridge only once?

2. If this is possible, what are the start and end points within the workshop for cleaning process?

 

Possible Answers:

  1. It is not possible to clean up all the bridges without crossing bridge number 7 more than once.
  2. It is not possible to clean up all the bridges without crossing bridge number 8 more than once.
  3. It is not possible to clean up all the bridges without crossing bridge number 9 more than once.
  4. It is possible if the elves start at A and end at B.
  5. It is possible if the elves start at A and end at C.
  6. It is possible if the elves start at A and end at D.
  7. It is possible if the elves start at A and end at E.
  8. It is possible if the elves start at B and end at C.
  9. It is possible if the elves start at B and end at D.
  10. It is possible if the elves start at C and end at D.
Challenge as PDF