
© Julia Nurit Schönnagel, MATH+
Autor: Dante Luber (BMS, Goethe Universität Frankfurt )
Aufgabe
Die Elfen, die fleißig Geschenke für den Weihnachtsmann einpacken, möchten in ihrer Freizeit Fußball spielen. Sie haben den Weihnachtsmann mehrfach um einen Fußball gebeten, doch aufgrund des knappen Budgets in diesem Jahr weigert er sich, einen zu kaufen. Ein schlauer Elf namens Mo, der Geschenkboxen herstellt, hat die brillante Idee, den Fußball selbst zu basteln. Mo hat Zugang zu einer Maschine, die verschiedene Körpernetze (2D-Formen) auf festes Papier drucken kann.
Mo ist sich jedoch unsicher, welches Netz er drucken soll, damit es zu einem Ball gefaltet und zusammengeklebt werden kann. Daher fragt er die schlaue Elfe Mara um Rat.
Mara antwortet: “Ich kann dir kein Design garantieren, das einen perfekten Ball ergibt, aber ich kenne ein cooles Objekt, das ihr zum Spielen verwenden könnt.”
Sie zeigt Mo ein Bild des Körpers, den sie für das Spiel basteln können (siehe Abbildung 1).
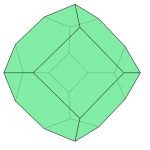
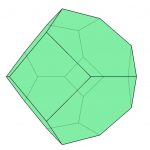
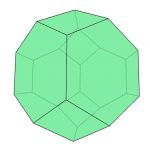
Abbildung 1: Drei 3D-Bilder des finalen Fußballs aus verschiedenen Blickwinkeln
Begeistert fragt Mo Mara nach dem Entwurf des Designs. Mara geht ins Büro und sucht in ihrem Computer nach der Datei von dem Netz für diesen Körper. Leider kann sie sich nicht mehr erinnern welche Nummer der Entwurf hat. Sie ist sich aber sicher, dass er sich unter diesen 8 Entwürfen befindet und druckt alle 8 möglichen Netze aus. Mo muss selbst herausfinden welches der unten gezeigten Netze zu dem Objekt in Abbildung 1 passt.
Welches Netz (1) bis (8) muss Mo wählen, sodass es zu diesem Objekt gefaltet werden kann?

Netz 1
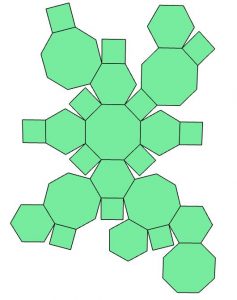
Netz 2
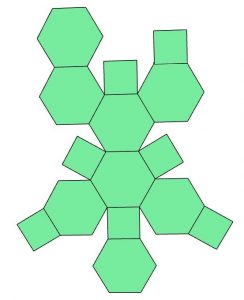
Netz 3
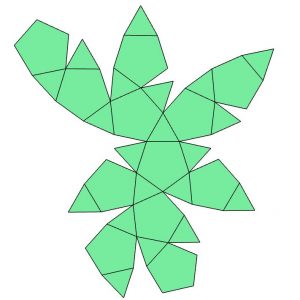
Netz 4
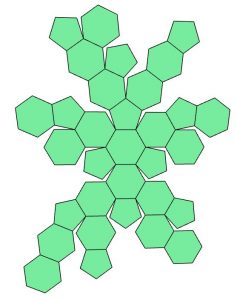
Netz 5
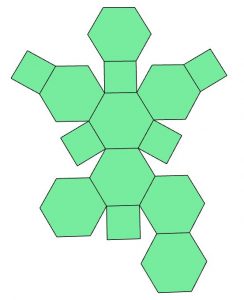
Netz 6
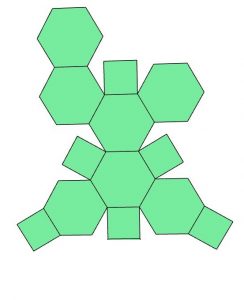
Netz 7

Netz 8
Antwortmöglichkeiten:
- Netz 1
- Netz 2
- Netz 3
- Netz 4
- Netz 5
- Netz 6
- Netz 7
- Netz 8
- Alle
- Keines
Projektbezug:
- Die Abbildungen wurden mit OSCAR erstellt — Open Source Computer Algebra Research System, Version 1.0.0, entwickelt vom OSCAR-Team, 2024.
- Das OSCAR-Projekt wird im Rahmen des TRR 195 zu einem visionären Open-Source-Computeralgebrasystem der nächsten Generation entwickelt, das die kombinierten mathematischen Fähigkeiten der zugrunde liegenden Systeme übertrifft.
- OSCAR ermöglicht es Nutzern, neue mathematische Objekte effizient zu konstruieren, indem vorhandene Bausteine aus den einzelnen Kernkomponenten kombiniert werden. Diese Objekte erhalten dadurch mathematische Fähigkeiten, die über die der individuellen Systeme hinausgehen, auf eine transparente Weise.
- Für weitere Informationen oder wenn Sie Oscar selbst nutzen möchten, besuchen Sie https://www.oscar-system.org.
- Diese Aufgabe wurde inspiriert von MatchTheNet, einem kostenlosen Online-Spiel zur polyhedralen Geometrie, das vom polymake-Team entwickelt wurde. Sie können das vollständige Spiel unter https://www.matchthenet.de spielen