21 Wise Thanks to AI?

© Ivana Martic, MATH+

Authors: Moritz Grillo, Martin Skutella

Project: AA3-12: On the Expressivity of Neural Networks

Challenge

In ancient times, there was a story of three wise men guided by a star to a specific location—a tale passed down for generations.
This idea of a star leading people to an exact spot had always baffled high school senior Geoffrey. He didn’t put much stock in the centuries-old tale, dismissing it as little more than an ancient “urban legend.” But the logistics of the star left him curious. Even without modern light pollution, how could a faraway celestial object possibly serve as a precise guide?

Determined to modernize the concept, Geoffrey and his friend John decided to bring some tech flair to their town’s holiday play. Using artificial intelligence, they designed a small neural network and packaged it as a smartphone app. The app was handed to the three actors playing the wise men, who were chosen by the local event organizer. Unfortunately, the chosen actors neither fit the “wise” nor the “reliable” description.

Chantalle, on the other hand, who had been cast as the leading role of Mary, was much more engaged. According to the organizer’s directions, her role was to stay silent, looking serene while her on-stage husband, Joseph, did most of the talking. Frustrated by this outdated division of roles, Chantalle decided to channel her energy elsewhere: helping ensure the so-called ‘wise men’ could actually find their way to the target destination. She had her reasons, too—she was eager to wrap up the play and step away from her silent role as quickly as possible.

“It’s actually pretty straightforward,” John explained. “You enter the x– and y-coordinates of your location into the neural network, and it calculates a non-negative value z. The closer you are to the target spot, the larger z will be.”

“And how does the neural network calculate z?” Chantalle asked with interest. “And what value of z means you’ve reached the target?” Geoffrey eagerly pulled out a detailed diagram to show her the inner workings of their neural network:

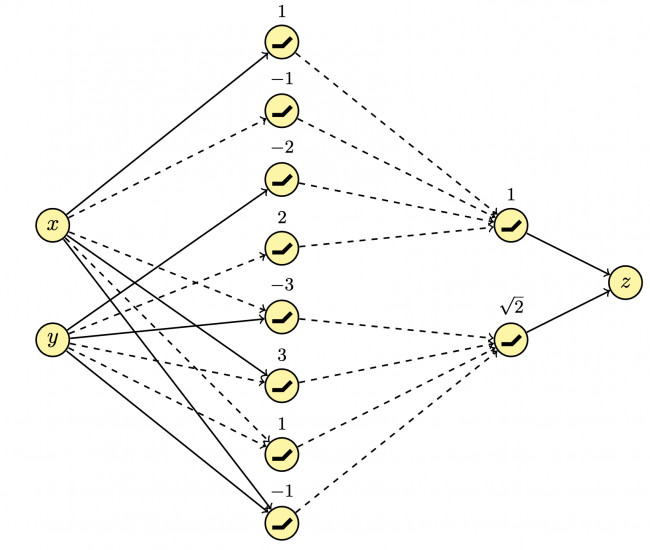
“The network consists of interconnected neurons,” Geoffrey explained, “which are represented here as yellow circles, and their connections as arrows. The neurons labeled x and y on the left are input neurons, where the values of the x– and y-coordinates are entered. The neuron labeled z on the right is the output neuron, which outputs the value z. Between them are two layers of hidden neurons, where the actual computation takes place. The first layer consists of eight, and the second of two hidden neurons.”

John continued: “To compute the values of neurons in one layer, you need the values of the neurons in the previous layer. These are passed to the next layer via the arrows. A solid arrow transmits the value of a neuron to the neuron in the next layer. A dashed arrow also transmits this value but flips the sign, i.e., multiplies it by -1. The receiving neuron adds all the values transmitted by the incoming arrows to the number written above the neuron. The value of the receiving neuron is then the maximum of 0 and this sum. For example, if x and y are the values of the input neurons, the values of the eight hidden neurons in the first layer are (from top to bottom):

\max\{0,x+1\}\max\{0,-x-1\}\max\{0,y-2\}\max\{0,-y+2\}\max\{0,-x+y-3\}\max\{0,x-y+3\}\max\{0,-x-y+1\}\max\{0,x+y-1\}

The values of the two hidden neurons in the second layer are calculated similarly from the values of the hidden neurons in the first layer. The value z output by the output neuron is the sum of the values of the two hidden neurons in the second layer.”

Fascinated, Chantalle studied the sketch, trying to grasp the intuitive meaning of the network’s neurons. Geoffrey suggested she figure out for which coordinate pairs x,y the two hidden neurons in the second layer take a strictly positive value. “From that, you can immediately determine for which pairs x,y the resulting output z is strictly positive,” he said.
When Chantalle eventually drew a sketch on her notepad, Geoffrey recognized it and knew she had understood.

“And now I also know at which coordinate pair (x,y) the three kings will find the manger, and what the maximum value for z is there,” said Chantalle, her devout expression replaced by a satisfied grin.

Task

Determine
i) which of the sketches S1 through S9 in Figure 1a) below is correct,
ii) which of the values W1 through W9 in Figure 1b) below is the correct maximum value for z, and
iii) which coordinate pair P1 through P9 in Figure 1c) below corresponds to this maximum value.

a) Possible sketches of the region in the x–y plane where z > 0 (Note, that the sketches are to scale):

b) Possible maximum values for z:

c) Possible coordinate pairs (x, y) where the maximum value is attained:

Figure 1: Possible sketches, values, and coordinate pairs.

In which of the answer options 1 to 10 does the correct triplet consisting of sketch, value, and coordinate pair appear?

Possible Answers:

1. (S1,W1,P1) or (S2,W2,P2) or (S3,W3,P3) or (S4,W4,P4)
2. (S5,W5,P5) or (S6,W6,P6) or (S7,W7,P7) or (S8,W8,P8)
3. (S9,W9,P9) or (S1,W3,P1) or (S2,W4,P2) or (S3,W5,P3)
4. (S4,W6,P4) or (S5,W7,P5) or (S6,W8,P6) or (S7,W9,P7)
5. (S8,W1,P8) or (S9,W2,P9) or (S1,W2,P3) or (S2,W3,P3)
6. (S3,W4,P5) or (S4,W5,P6) or (S5,W6,P7) or (S6,W7,P8)
7. (S7,W8,P9) or (S8,W9,P1) or (S9,W1,P2) or (S1,W5,P4)
8. (S2,W7,P5) or (S3,W6,P6) or (S4,W8,P7) or (S5,W9,P8)
9. (S6,W1,P9) or (S7,W2,P1) or (S8,W3,P2) or (S9,W4,P3)
10. (S1,W9,P5) or (S2,W8,P6) or (S3,W7,P5) or (S4,W6,P8)

Project Reference:

In our MATH^+ research project titled On the Expressivity of Neural Networks, we are working on a better structural understanding of neural networks. Similar to Chantalle in our story, we aim to understand the properties of a given neural network. Furthermore, we explore which structures a neural network should have in order to compute certain functions exactly. One of our results, for example, states that neural networks with many hidden layers can have significantly more complex decision patterns (the regions where the neural network takes on a positive value) than neural networks with fewer hidden layers.

A few weeks ago, Geoffrey Hinton from the University of Toronto (Canada) and John Hopfield from Princeton University (USA) were awarded the Nobel Prize “for fundamental discoveries and inventions that enable machine learning with artificial neural networks“.