
© Ivana, Martić MATH+
Autor: Christian Haase
Projekt: AA3-12
Aufgabe
Die Wichtel stellen Geschenkkarten aus Karopapier her, das sie normalerweise für Berechnungen verwenden, und fertigen diese für Kinder in verschiedenen Formen an. Um die Produktion zu erleichtern, hat der Weihnachtsmann vorgeschrieben, dass alle Karten die Form eines geschlossenen konvexen Polygons annehmen müssen, wobei alle Eckpunkte des Polygons Kreuzungspunkte auf dem Karopapier sein müssen.
“Konvex” bedeutet hier, dass man entlang des Weges nur Linkskurven machen kann, und ” Eckpunkte” bedeutet, dass der Wichtel an diesen Stellen beim Ausschneiden der Karte die Richtung ändern muss. Diese Vorgaben schließen bestimmte Formen aus:
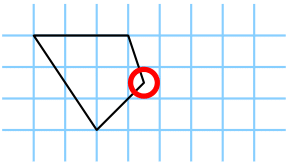
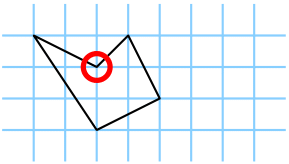
Abbildung 1: Zwei Beispiele für verbotene Karten: Die erste hat keine richtigen Eckpunkte und die zweite ist nicht konvex. Beide Karten sind laut Definition verboten
Das erste Bild in Abbildung 1 zeigt eine konvexe Karte, bei der ein Eckpunkt kein Kreuzungspunkt des Karopapiers ist, und das zweite Bild zeigt ein Beispiel für eine nicht-konvexe Karte.
Der Weihnachtsmann bezeichnet mit b die Anzahl der Kreuzungspunkte entlang des Randes der Karte und mit i die Anzahl der Kreuzungspunkte im Inneren der Karte.
Für jedes solcher Polygone wird die eingeschlossene Fläche mit a bezeichnet, wobei die Seitenlänge eines Quadrats auf dem Karopapier 1 Dezimeter beträgt.
Nun führt der Weihnachtsmann für die Karten die Kurzschreibweise (b,i,a) ein. Zum Beispiel hätte eine Geschenkkarte wie in Abbildung 2 (a) genau b=3 Kreuzungspunkte auf dem Rand, i=0 innere Kreuzungspunkte und eine Fläche von a=0.5. Die zugehörige Kurzschreibweise lautet dann ( 3, 0, 0.5) . Ebenso kann eine Karte mit den Werten (9, 1, 4.5) in Abbildung 2 (b) beobachtet werden.
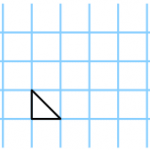
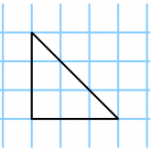
Abbildung 2: Beispiele für gültige Karten
Die Wichtel sind nun besorgt, dass einige Geschenkkarten möglicherweise nicht mehr hergestellt werden können. Welche der folgenden Karten mit den Tripeln (b, i, a) können sie weiterhin erstellen
- (24, 16, 27)
- (15, 7, 13.5)
- (3, 9, 9.5)
- (18, 0, 9)
Antwortmöglichkeiten:
- (ja, ja, ja, ja)
- (ja, ja, nein, ja)
- (ja, ja, ja, nein)
- (ja, nein, ja, ja)
- (nein, ja, ja, ja)
- (nein, ja, nein, ja)
- (ja, nein, ja, nein)
- (nein, nein, ja, ja)
- (nein, nein, nein, ja)
- (nein, nein, nein, nein)
Projektreferenz:
Das Projekt zielt darauf ab, unser Verständnis der Ausdruckskraft neuronaler Netze (NNs) zu vertiefen. Insbesondere werden sowohl untere als auch obere Schranken für die topologische Vereinfachung untersucht, die ein ReLU-Neuronales Netz bei gegebener Architektur erreichen kann.
Im Kontext allgemeiner Darstellungen von Funktionen beobachten wir, dass die von einem ReLU-Netzwerk berechnete Funktion stückweise linear und kontinuierlich (CPWL) ist, da sie eine Komposition aus affinen Transformationen und der ReLU-Funktion ist. Andererseits ist bekannt, dass jede CPWL-Funktion durch ein ReLU-Netzwerk logarithmischer Tiefe dargestellt werden kann. In [1] wurde vermutet, dass diese logarithmische Schranke scharf ist. Mit anderen Worten: Es könnte CPWL-Funktionen geben, die nur durch ReLU-Netzwerke logarithmischer Tiefe dargestellt werden können.
Diese Vermutung wurde unter einer natürlichen Annahme für die Dimension n = 4 unter Verwendung von Techniken der gemischt-ganzzahligen Optimierung bewiesen. Zusätzlich wurde in [2] gezeigt, dass logarithmische Tiefe erforderlich ist, um das Maximum von n Zahlen zu berechnen, wenn nur ganzzahlige Gewichte erlaubt sind. Dieses Ergebnis basiert auf der Dualität zwischen neuronalen Netzwerken und Newton-Polytopen durch tropische Geometrie. Ein primäres Ziel dieses Projekts ist es, die Vermutung entweder zu beweisen oder zu widerlegen.
[1] Christoph Hertrich, Amitabh Basu, Marco Di Summa, und Martin Skutella. Towards lower bounds on the depth of ReLU neural networks.
SIAM Journal on Discrete Mathematics, 37(2):997–1029, 2023.
[2] Christian Haase, Christoph Hertrich und Georg Loho. Lower bounds on the depth of integral ReLU neural networks via lattice polytopes, 2023