12 Kabel-Chaos

© Julia Nurit Schönnagel, MATH+

Autor: Lukas Protz (TU Berlin, MATH+)

Aufgabe

Paula und Quentin sind die Chefelfen der IT-Abteilung am Nordpol. Normalerweise läuft in der Abteilung alles nach Plan, aber eines Tages erhalten sie Nachrichten von zwei der dort arbeitenden Elfen. Diese beschweren sich über Probleme bei der Verbindung zum Winternet (dem Äquivalent des Internets am Nordpol).

Da die Verbindung zum Winternet über Kabel erfolgt, vermuten Paula und Quentin, dass einige der Kabel beschädigt sein könnten, und gehen daher in den Kabelraum, um diese zu überprüfen. Die Kabelanschlüsse, die zu den beiden Elfen gehören, sind mit “\frac{22}{7}” und “\frac{87}{32}”  beschriftet. Beachte, dass die Beschriftungen der Kabel zwar in Form von Brüchen sind, aber (a priori) keinen Zusammenhang mit rationalen Zahlen haben.

Im Kabelraum angekommen, stehen Paula und Quentin vor einem riesigen Kabelbaum und sind überwältigt. Wie sollen sie bloß die beiden Kabelanschlüsse finden, die sie suchen? Zum Glück finden sie eine Notiz und ein Bild (siehe Abbildung 1) an der Wand, die erklären, wie die Anschlüsse beschriftet sind:

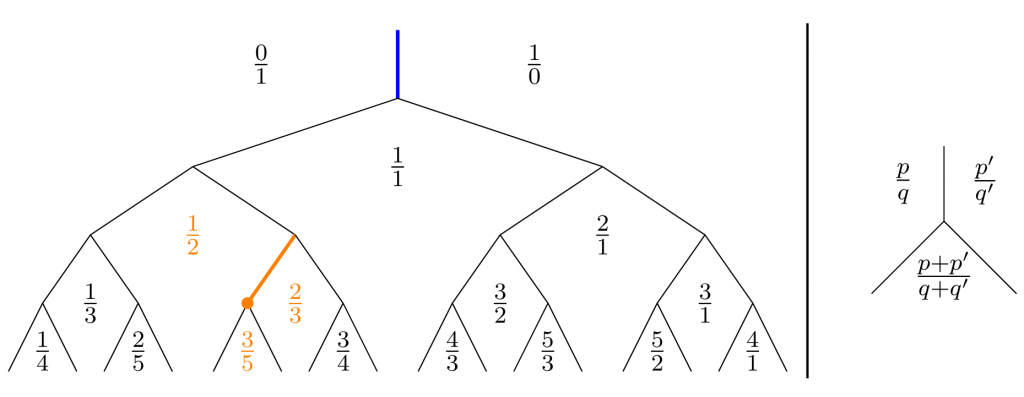
Abbildung 1: Links: Die Wurzeln des Baums mit den entsprechenden Beschriftungen. Rechts: Die Regel, um eine neue Beschriftung zu erhalten, wenn sich eine Wurzel aufteilt und ein Kabel endet. Der orange Punkt kennzeichnet das Ende des Kabels mit der Beschriftung “\frac{3}{5}“.

1. 1. Die Kabel sind in einer Baumstruktur (dem Kabelbaum) angeordnet, siehe Abbildung 1. Die Kabelbündel sind die einzelnen Wurzeln (Kanten) des Kabelbaums. Es gibt eine Hauptwurzel des Baums, die im Bild blau gefärbt ist.
   2. Der Bereich links von der Hauptwurzel ist mit “\frac{0}{1}” , der Bereich rechts davon mit “\frac{1}{0}” beschriftet.
   3. Jedes Mal, wenn sich eine Wurzel in zwei neue Wurzeln aufteilt, endet ein Kabel, und die anderen setzen sich entlang einer der beiden neuen Wurzeln fort.
   4. Die Hauptwurzel teilt sich in zwei neue Wurzeln. Das Kabel, das an diesem Teilungspunkt endet, trägt die Beschriftung “\frac{1}{1}“, die wie folgt aus den Beschriftungen des linken und rechten Bereichs gebildet wird:

      \frac{0 + 1}{1 + 0} = \frac{1}{1}.

      Der durch die beiden neuen Wurzeln neu geschaffene Bereich wird ebenfalls mit “\frac{1}{1}” beschriftet.

   5. Dieser Prozess geht unendlich weiter. Jede Wurzel teilt sich in zwei neue Wurzeln, ein Kabel endet und ein neuer Bereich wird geschaffen. Wenn die Beschriftungen des rechten und linken Bereichs der Wurzel vor dem Teilungspunkt “\frac{p}{q}” und “\frac{p'}{q'}” lauten, dann wird das endende Kabel und der neue Bereich mit “\frac{p''}{q''}” beschriftet, gemäß der folgenden Regel:

      \frac{p''}{q''} = \frac{p + p'}{q + q'}.

   6. Zum Beispiel lauten die Beschriftungen der Bereiche links und rechts der in orange hervorgehobenen Wurzel in Abbildung 1 “\frac{1}{2}” und “\frac{2}{3}“, und die Beschriftung des neuen Bereichs sowie des endenden Kabels am orangefarbenen Punkt lautet

      \frac{1 + 2}{2 + 3} = \frac{3}{5}.

Um die gesuchten Kabel zu finden, starten Paula und Quentin von der Hauptwurzel. Jedes Mal, wenn sich eine Wurzel teilt, folgen sie entweder der linken oder der rechten Wurzel, bis sie an einem Teilungspunkt für eines der gesuchten Kabel ankommen. Kannst du Paula und Quentin helfen, die Enden der Kabel mit den Beschriftungen “\frac{22}{7}” und “\frac{87}{32}” zu finden, indem du die Summe der Rechtsabbiegungen und die Summe der Linksabbiegungen bestimmst?

Beispiel: Um von der Hauptwurzel zu dem Teilungspunkt zu gelangen, an dem das Kabel mit der Beschriftung “\frac{3}{5}” endet, müssen sie zuerst nach links, dann nach rechts und schließlich wieder nach links abbiegen.

Hinweis: Um unsere Terminologie rund um linke und rechte Bereiche zu klären, definieren wir diese Konzepte relativ zur Hauptwurzel. Definiere den Abstand eines Teilungspunkts von der Hauptwurzel als die Anzahl der Teilungspunkte entlang des Pfades von der Hauptwurzel zu diesem Teilungspunkt, durch die Zwischenwurzeln im Kabelbaum hindurch. Zum Beispiel hat der Teilungspunkt mit der Beschriftung “\frac{1}{2}” einen Abstand von 2 zur Hauptwurzel.

Ein Teilungspunkt wird als näher an der Hauptwurzel liegend bezeichnet als ein anderer, wenn sein Abstand zur Hauptwurzel kleiner ist als der des anderen Punktes.

Jede Wurzel verbindet zwei Teilungspunkte, von denen einer näher an der Hauptwurzel liegt. Wenn man sich von dem Teilungspunkt, der weiter von der Hauptwurzel entfernt ist, zu dem bewegt, der näher liegt, wird der linke Bereich als der Bereich definiert, der in Richtung einer 90^\circ-Drehung gegen den Uhrzeigersinn zur Bewegungsrichtung liegt, während der rechte Bereich in Richtung einer 90^\circ-Drehung im Uhrzeigersinn liegt. Die linke Wurzel ist diejenige der neuen Wurzeln an einem Teilungspunkt, die an den linken Bereich angrenzt. Analog ist die rechte Wurzel diejenige der neuen Wurzeln, die an den rechten Bereich angrenzt.

Antwortmöglichkeiten

1. 6 Links- und 8 Rechtsdrehungen
2. 11 Links- und 8 Rechtsdrehungen
3. 8 Links- und 9 Rechtsdrehungen
4. 10 Links- und 9 Rechtsdrehungen
5. 7 Links- und 10 Rechtsdrehungen
6. 9 Links- und 10 Rechtsdrehungen
7. 8 Links- und 11 Rechtsdrehungen
8. 7 Links- und 12 Rechtsdrehungen
9. 6 Links- und 13 Rechtsdrehungen
10. Nicht beide Beschriftungen erscheinen im Baum.