
© Ivana Martic, MATH+
Authors: Pim van ‘t Hof, Stefano Piceghello (University of Twente)
Project: 4TU.AMI
Challenge
Pixies Pi and Pie are baking perfectly round Christmas cookies. Using a circular cookie cutter, they cut out four identical cookies from a large circular piece of dough. Figure 1 shows the piece of dough that remains after the cookies have been put in the oven. The figure also shows two perpendicular diameters AB and CD of the large circle. Diameter AB is tangent to the boundary of one of the circular holes. Line segment EF is a chord of the large circle that is tangent to the boundary of the same hole and parallel to diameter AB. The length of EF is 36 cm.
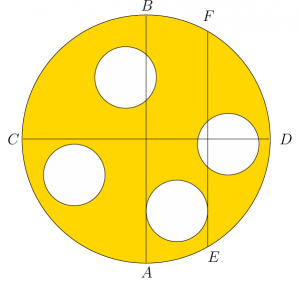
Figure 1: The remaining piece of dough.
What is the area of the remaining piece of dough?
Possible Answers
- 244\pi cm^2
- 300\pi cm^2
- 312\pi cm^2
- 320\pi cm^2
- 324\pi cm^2
- 344\pi cm^2
- 360\pi cm^2
- 368\pi cm^2
- 381\pi cm^2
- There is not enough information in the problem statement to compute the area of the remaining piece of dough.