
© Christoph Graczyk, MATH+
Autoren: Olaf Parczyk, Silas Rathke (FU Berlin)
Projekt: Learning Extremal Structures in Combinatorics (EF 1-12)
Aufgabe
Dieses Jahr findet die Frauen-Eisfußball-Weltmeisterschaft am Südpol statt. Allerdings wird “Down Under” nicht so häufig Eisfußball gespielt wie am Nordpol. Deswegen sind die Eisfußballstadien dort ein wenig in die Jahre gekommen.
Das musste auch Stadionmeisterin Martina am eigenen Leib erfahren: Kaum ging sie über das Eisfußball-Feld, da brach sie direkt in das Eis ein. Nachdem sie ihre Füße getrocknet und sich von dem Schock erholt hat, beschließt sie, das gesamte Eisfußball-Feld abzugehen, um zu sehen, ob das Eis noch an anderen Stellen instabil ist.
Dazu teilt sie das Feld wie folgt in ein 4\,\times\,9 – Gitter auf:
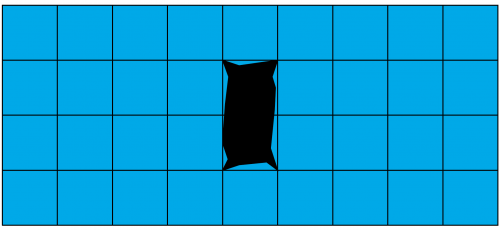
Abbildung 1: Das 4 \times 9 Eisfußball-Feld mit Martinas Einbruchstelle.
Die beiden Quadrate in der Mitte bilden die Stelle, wo sie ins Eis eingebrochen ist. Diese beiden Quadrate kann sie nicht mehr betreten. Alle anderen Quadrate möchte sie aber nun auf Stabilität testen.
Dazu möchte sie auf einem beliebigen Quadrat des Fußballfelds anfangen und möglichst viele Quadrate eins nach dem anderen abgehen, ohne dabei jemals das Spielfeld zu verlassen. Außerdem darf sie kein Quadrat betreten, welches sie vorher schon einmal besucht hat. Nur am Ende möchte sie wieder bei dem Quadrat ankommen, wo sie angefangen hat. Das ist aber die einzige Ausnahme, wo ein Quadrat zwei Mal betreten werden darf. (Anmerkung des Autors: Warum sie sich diese bekloppten Regeln überlegt hat, weiß ich leider nicht. Diese Geschichte wurde über mehrere Stellen vom Südpol nach Deutschland überliefert und es kann gut sein, dass sich im Laufe der Zeit einige Details geändert haben.)
Es kommt noch erschwerend hinzu, dass sie nach dem Sturz ins Eis humpelt. Das bedeutet, dass sie abwechselnd einen langen und einen kurzen Schritt machen muss. Bei einem langen Schritt muss sie zu einem Quadrat gehen, welches beim Schach einen “Springer-Zug” entfernt ist. Nach einem langen Schritt landet Martina also auf einem Feld, welches zwei Schritte horizontal und ein Schritt vertikal entfernt ist, oder zwei Schritte vertikal und ein Schritt horizontal, wie in Abbildung 2 veranschaulicht wird: (Anmerkung des Autors: An dieser Stelle mag sich der kritische Leser zurecht fragen, ob das Eisfußballfeld wirklich so klein ist, dass man mit vier langen Schritten von einem Quadrat ganz links zu einem Quadrat ganz rechts kommen kann. Ja, das ist es. Und wieder weiß ich leider nicht, warum das so ist. Wie gesagt, diese Geschichte wurde schon so häufig erzählt, dass sich die Details möglicherweise geändert haben…)
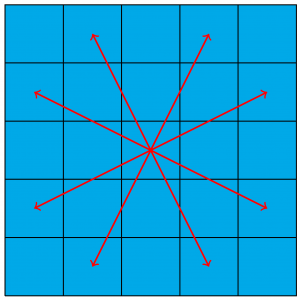
Abbildung 2: Alle Möglichkeiten für einen langen Schritt ausgehend vom Quadrat in der Mitte.
Bei einem kurzen Schritt muss sie zu einem waagerecht oder senkrecht benachbarten Quadrat gehen, wie in Abbildung 3 veranschaulicht wird:

Abbildung 3: Alle Möglichkeiten für einen kurzen Schritt ausgehend vom Quadrat in der Mitte.
Eine mögliche Schrittfolge könnte also wie in Abbildung 4 aussehen.
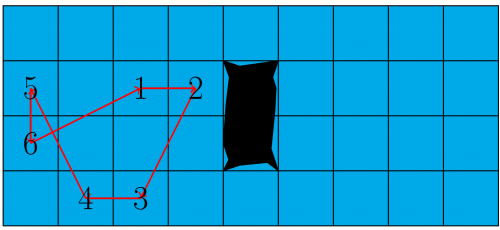
Abbildung 4: Ein möglicher Weg für Martina.
Bei dieser Schrittfolge ist sie sechs Quadrate abgelaufen.
Was ist die größte Zahl an Quadraten, die sie mit einer Schrittfolge ablaufen kann?
Alle Bedingungen zusammengefasst:
- Das Feld hat zwei Löcher, die nicht betreten werden dürfen.
- Martina darf ihr Startfeld beliebig wählen.
- Sie macht abwechselnd einen langen und einen kurzen Schritt.
- Sie betritt kein Feld doppelt, außer das Startfeld, auf dem sie ihre Schrittfolge beendet.
Antwortmöglichkeiten
- 34
- 33
- 32
- 31
- 30
- 29
- 28
- 27
- 26
- Weniger als 26
Projektbezug
Im Projekt “Learning Extremal Structures in Combinatorics” verwenden wir Ansätze aus dem Bereich der künstlichen Intelligenz und des maschinellen Lernens, um neue Konstruktionen für Graphen mit bestimmten Eigenschaften zu finden.
Die vorliegende Aufgabe lässt sich gut als extremales Problem in der Graphentheorie formulieren, ähnlich wie die Probleme, die wir in diesem Projekt studieren.