19 Dreiecksspiel

© Vira Raichenko, MATH+

Autor*innen: Hajo Broersma, Jesse van Rhijn (University of Twente)

Projekt: 4TU.AMI

Aufgabe

In ihrer Freizeit spielen einige der Elfen des Weihnachtsmanns gerne ein Spiel, das sie “Fortgeschrittenes Tauziehen” nennen. Bei diesem Spiel werden die Elfen in zwei (möglicherweise ungleich große) Teams aufgeteilt, die sich durch gelbe und blaue Hüte unterscheiden. Alle teilnehmenden Elfen stehen in einem Kreis und verbinden sich untereinander mit Seilen, sodass je zwei Elfen durch ein Seil verbunden sind.  Jedes Team versucht das andere Team durch Ziehen an den Seilen auf ihre Seite zu ziehen.

Die Seile, die für dieses Spiel verwendet werden, können eine von zwei Farben haben, rot oder grün. Allerdings hat die Farbe eines Seils keine Bedeutung für das Spiel und kann beliebig gewählt werden. Eine zuschauende Elfe bemerkt, dass es manchmal, besonders wenn viele Elfen teilnehmen, vorkommt, dass drei Elfen aus einem Team alle untereinander mit Seilen der gleichen Farbe verbunden sind. Wir nennen dies ein perfektes Dreieck, siehe Abbildung 1 für ein Beispiel.

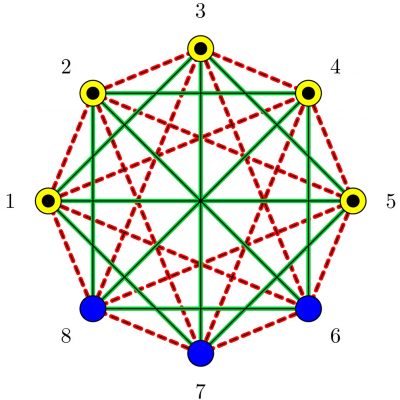
Abbildung 1: Ein Beispiel für ein fortgeschrittenes Tauziehspiel mit acht Elfen. Grüne Seile sind als durchgezogene Linien, rote Seile als gestrichelte Linien gezeichnet. Blaue Punkte stellen Elfen mit einem blauen Hut dar, gelbe Punkte (mit schwarzem Punkt in der Mitte) stellen Elfen mit einem gelben Hut dar. Die Elfen 1, 3 und 5 bilden ein perfektes Dreieck: Sie sind paarweise miteinander durch grüne Seile verbunden, und jeder von ihnen trägt einen gelben Hut.

Was ist die kleinste Anzahl von Elfen, die an einem fortgeschrittenen Tauziehen teilnehmen müssen, damit es garantiert ein perfektes Dreieck gibt?

Antwortmöglichkeiten

1. Sechs Elfen.
2. Sieben Elfen.
3. Acht Elfen.
4. Neun Elfen.
5. Zehn Elfen.
6. Elf Elfen.
7. Zwölf Elfen.
8. Dreizehn Elfen.
9. Vierzehn Elfen.
10. Solch eine Zahl existiert nicht (wir können Farben immer so zuweisen, dass wir ein perfektes Dreieck vermeiden).