
© Zyanya Santuario, MATH+
Autor: Dion Gijswijt (TU Delft)
Projekt: 4TU.AMI
Aufgabe
Aktuell ist der Weihnachtsmann auf einer Mission, um Geschenke an Kinder zu verteilen. Seine Reise erstreckt sich über sechs Städte, die mit A bis F bezeichnet sind. Ausgehend von der Werkstatt des Weihnachtsmanns (WdW) muss er eine der Städte A, B, C, D, E oder F auswählen, um seinen Besuch zu beginnen.
Die Rentiere sind müde vom Spielen und können deswegen keine langen Strecken mehr zurücklegen. Das erfordert, dass der Weihnachtsmann die kürzeste Route plant. Er hat eine Karte, die Flugentfernungen zwischen den Städten entlang verbindender Linien anzeigt, und die Kreise zeigen die Entfernungen von der Werkstatt WdW zu jeder Stadt an.
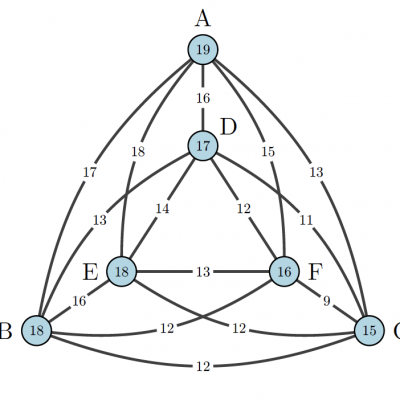
Der Weihnachtsmann muss nun die kürzeste Abfolge für den Besuch der Städte wählen, bevor er zur Werkstatt des Weihnachtsmanns zurückkehrt. Wenn er beispielsweise die Route WdW-F-A-E-B-C-D-WdW nimmt, ist die Tour 16+15+18+16+12+11+17=105 lang.
Was ist die Länge der kürzesten Tour, die der Weihnachtsmann nehmen kann?
Antwortmöglichkeiten
- 104
- 103
- 102
- 101
- 100
- 99
- 98
- 97
- 96
- 95