
© Vira Raichenko, MATH+
Autor: Matthew Maat (Universiteit Twente)
Projekt: Combining algorithms for parity games and linear programming
Aufgabe
Während ihrer langen Reise durch die Wüste sind die heiligen drei Könige beim Reiten ihrer Kamele eingeschlafen. Als sie aufwachen sind sie überrascht, denn sie können den Stern nicht mehr sehen. Tatsächlich ist der gesamte Himmel von einer großen Wolke bedeckt. Das muss die berüchtigte Al-Bermuda-Wolke sein. Eine Legende besagt, dass sie die Form eines gleichschenkligen rechtwinkligen Dreiecks hat, wobei die längste Seite 100 Kilometer lang ist. Solange sie sich unter der Wolke befinden, ist keine Orientierung möglich. Aber sobald es ihnen gelingt, aus der Wolke herauszukommen, werden sie es sofort bemerken, weil sie den Stern wieder sehen werden. Leider haben sie kaum noch Wasser. Je schneller sie der Wolke also entkommen können, desto besser. Es ist nur noch genug Wasser für 100 Kilometer übrig. Caspar wettet mit Melchior, dass er garantieren kann, dass sie die Wolke in weniger als 100 Kilometer Fußweg verlassen können und so hoffentlich nicht durstig werden, wenn sie seinem Rat folgen. Caspar beginnt, über seine Strategie nachzudenken. Wenn er einfach 100 Kilometer in einer geraden Linie geht, ist es möglich, dass sie sich jetzt in der unteren linken Ecke des Dreiecks befinden und zufällig genau nach rechts gehen (siehe Strecke AB in Abb. 1). Dann entkommen sie nicht innerhalb von 100 Kilometer. Stattdessen, wenn er in einem Kreis mit einem Umfang von 100 Kilometer geht, ist es möglich, dass sie im Punkt C gestartet sind (siehe Abbildung 1) daher das Dreieck ebenfalls nicht verlassen. Nach weiterem Nachdenken kommt er auf 4 weitere Strategien (siehe ebenfalls Abb. 1):
(a) Gehe 50 Kilometer geradeaus, mache eine Drehung von der Größe \alpha und gehe weitere 50 Kilometer geradeaus.
(b) Gehe x Kilometer geradeaus, mache eine 90^\circ-Drehung nach rechts, gehe dann geradeaus für 100 - 2x Kilometer, mache eine weitere Rechtsdrehung und gehe dann nochmals x Kilometer geradeaus.
(c) Das gleiche wie (b), aber diesmal machen wir bei der zweiten Drehung anstelle einer Drehung nach rechts eine Linksdrehung.
(d) Gehe z Kilometer geradeaus, mache eine Rechtsdrehung und gehe weitere 100 - z Kilometer geradeaus.
Angenommen, dass Caspar die richtigen Werte für die Parameter \alpha, x, y und z auswählt, sofern diese existieren, welche dieser Strategien kann Caspar verwenden, um sich selbst zu garantieren, die Wette zu gewinnen?
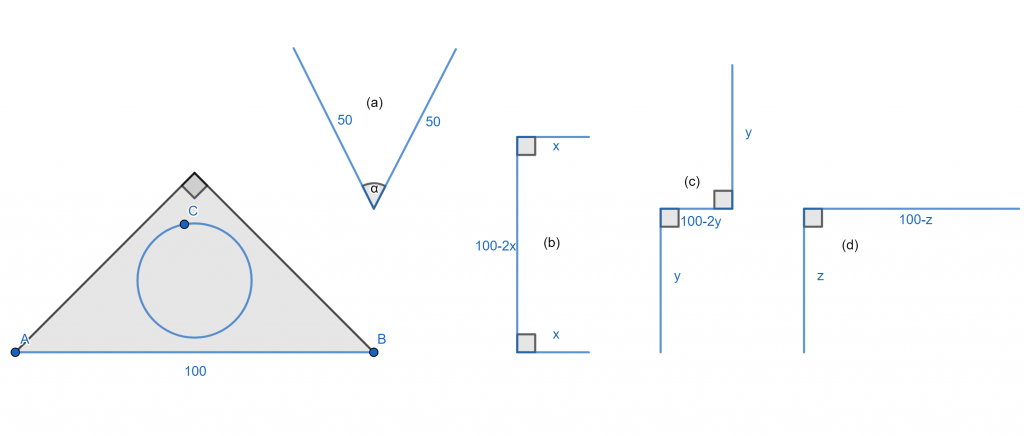
Abbildung 1: Links: Das Dreieck von Al-Bermuda. Rechts: Caspars Ideen für die zu nehmenden Routen.
Antwortmöglichkeiten
- Casper kann die Wette nicht garantiert gewinnen.
- Nur eine der vier Strategien
- Nur (a) und (b)
- Nur (a) und (c)
- Nur (a) und (d)
- Nur (b) und (c)
- Nur (b) und (d)
- Nur (c) und (d)
- Drei der vier Strategien
- Caspar kann die Wette mit allen Strategien garantiert gewinnen